【南京大学-软件分析】课程笔记

序言

返景入深林，复照青苔上。

越来越发现基础知识的重要，前一阵又跟着老师过了一遍，理解更加深入了，顺便整理笔记。

00 静态分析核心问题

以下参考啥玩应儿

核心问题：Abstraction和Over-approximation

1. Abstraction

   程序在动态运行时，有很多变量的值是动态变化的。

   比如一个是循环中，有一句new A()，那么每次循环都会在内存中生成一个A类对象，直到占满你的内存。

   这过程中的每一个A都是Concreate Object 也就是具体对象，是真真切切在内存中存在的。

   静态分析主要采用的方法就是为同一句new A() 只生成一个抽象的对象，也就是Abstract Object。

   这里你的抽象程度、抽象方式、静态分析的精度和速度都是不同的。

2. Over-approximation

   程序在动态执行时，其实根据输入的参数不同，执行的路径也会各不相同。

   随着程序规模和复杂度的增加，路径也就会变得无穷无尽。

   最终导致我们无法在有限的空间内枚举每一种执行路径，就会发生路径爆炸！

   为了可以在有限的空间内来枚举无限路径下的各种可能值，需要保守估计，也就是Over-approximation

   容忍一定程度的路径不敏感

01

PL：Programming Language

理论：语言设计，类型系统，语义和逻辑

环境：编译器，运行系统

应用：程序分析，程序验证，程序合成

技术：抽象解释（Abstract interpretation），数据流分析（Data-flow analysis），Hoare logic，Model checking，Symbolic execution等等

静态分析作用：程序可靠性、程序安全性、编译优化、程序理解（调用关系、类型识别）。

Soundness & Completeness

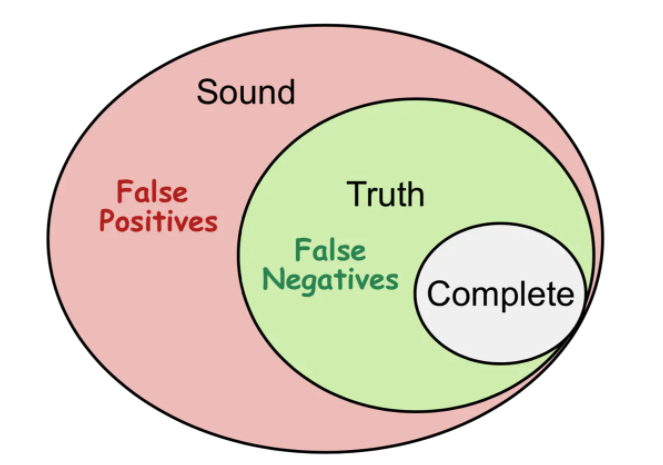
解释：

Truth：理论上的既sound又complete的概念。它代表着所有的程序的特点。假如说程序存在10个空指针应用的异常，那么truth的定义就是10，但是莱斯定理表明，并不存在这样的一个方法可以把这所有的10个异常都检查出来。Truth其实就是那个理论上的最优结果。

Sound：对程序进行过拟合，over-approximate，不会漏报，但是会有误报false positives

Complete：对程序进行欠拟合，under-approximate，不会误报，但是会有漏报false negatives

妥协soundness，相当于sound圈变小了，会造成漏报false negatives；

妥协completeness，相当于complete圈变大了，会造成误报false positives；

几乎所有的静态分析都会妥协completeness，宁愿误报也不要漏报！

很多重要领域如军工、航天领域，我们追求的是soundness，但是要平衡精度和速度。那么我们绝大多数软件分析方法都做到了completeness，那么只要能证明满足soundness，那么该分析方法就是正确的。

02

编译器与静态分析的关系

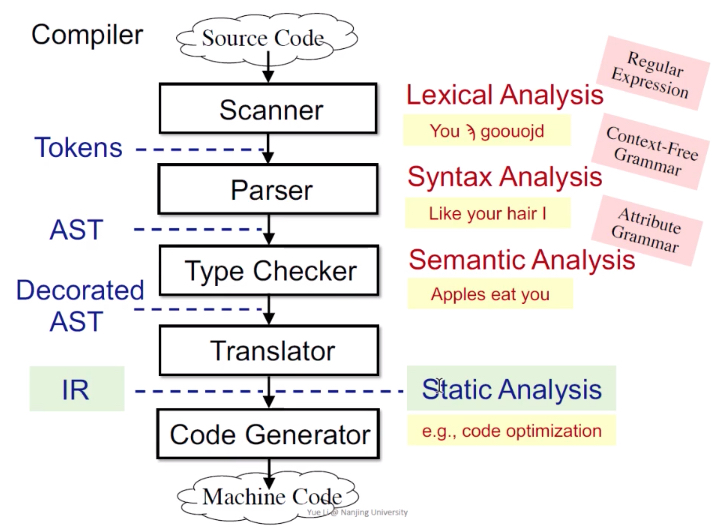
1. 源码

2. Scanner-词法分析LexicalAnalysis-正则表达式RegularExpression

   这一环中，判断每一个单词是否是合理的，合理的话就转换为Tokens，给下一步继续分析。

3. Parser-语法分析SyntaxAnalysis-上下文无关文法Context-Free Grammar

   这一环中，语法分析主要是判断语法是否合理，类似符合英语的“主谓宾”结构。

   这里用到一套形式化的结构就是上下文无关文法。

   生成语法树。

   为什么不用上下文敏感的语法来参与分析？

   答：就目前编程语言来说，上下文无关文法已经足够了。

   ​ 如果用上下文关联的语法，杀鸡用40米的牛刀，它更适合分析人讲的自然语言。

   ​ 弱表达能力的使用起来速度更快，效率更高。

4. Type Checker-语义检测Semantic Analysis-Attribute Grammar

   根据上一步生成的AST抽象语法树，编译器会进行一点特别简单的语义检查，例如Type-Checking类型检查。

   简单判断变量类型，例如float不能赋值给int。

   生成圣诞树。Decorated AST

5. Translator-生成中间表示代码IR-进行静态分析，优化

   IR普遍是三地址码，进行优化，安全检查。

   最后生成machine code机器码。

IR称为编译器前端，对于检查安全漏洞来说，必须要先把前端的检查都通过了，再去挑错，否则如果连基本的程序编译都无法通过，那么继续调漏洞也将毫无意义。

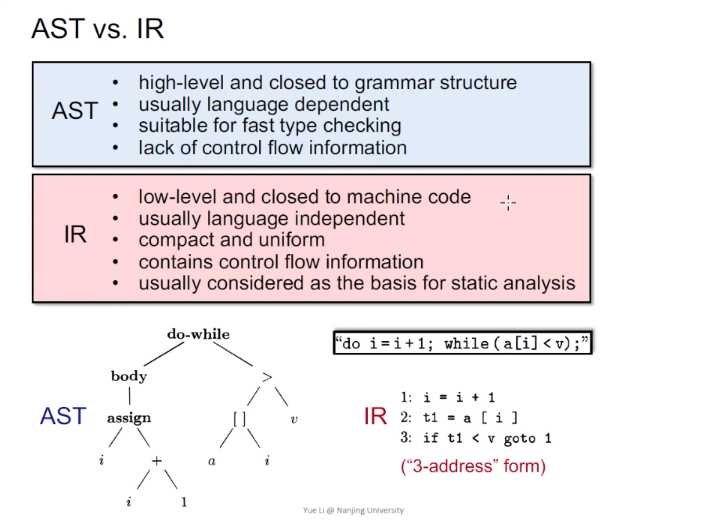
AST vs. IR

AST ：高级，更接近于语法结构，依赖于语言种类，适用于快速类型检查，缺少控制流信息。

IR：低级，更接近于机器码，不依赖语言种类，压缩且简洁，包含控制流信息。是静态分析的基础。

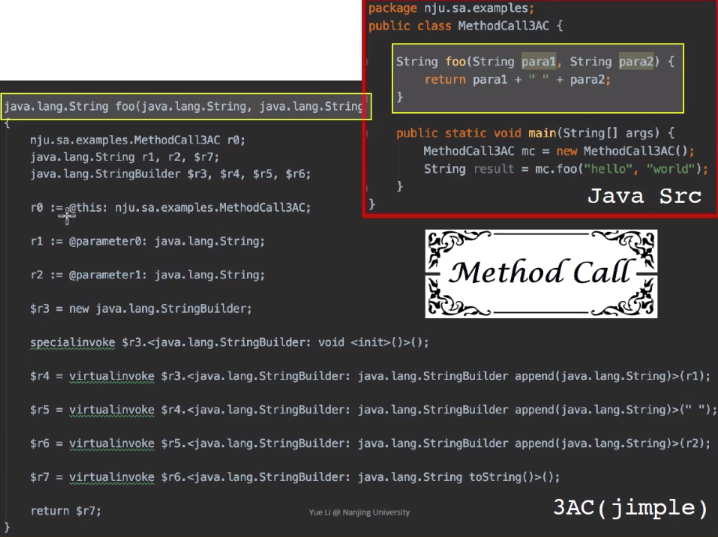
3AC-3地址码

soot

soot用得是typed 3AC 是在3AC内部存在类型的形式 Jimple：typed 3-address code

// java IR（Jimple）基本知识
invokespecial：call constructor, call superclass methods, call private methods
invokevirtual: instance methods call (virtual dispatch) 派生
invokeinterface: cannot optimization, checking interface implementation
invokestatic:call static methods

Java 7: invokedynamic -> Java static typing, dynamic language runs on JVM

method signature: class name, return type, method name(parameter1_type, parameter2_type)
  
clinit是类的初始化复制
  Class A{
   B b = ...//会调用B的clinit方法，给类属性复制

BasicBlock BB 基本块

定义：只有唯一1个开头入口和唯一1个结尾出口的最长3-地址指令序列。

识别基本块的算法：

首先确定入口指令，第一条指令是入口；

任何跳转指令的目标地址是入口；

任何跟在跳转指令之后的指令是入口。

然后构造基本块，任何基本块包含1个入口指令和其接下来的指令。

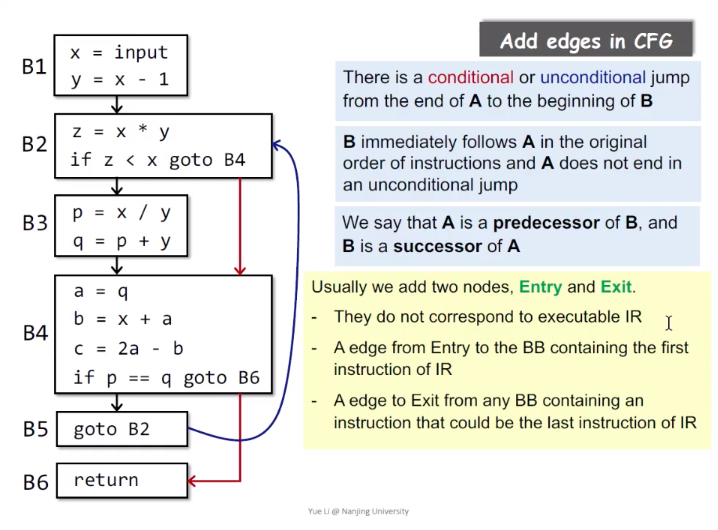
CFG Control Flow Graph

控制流边：

基本块A的结尾有跳转指令跳转到基本块B；

原始指令序列中，B紧跟着A，且A的结尾不是无条件跳转。

03

Data Flow Analysis

总结：

数学符号形式化表示；

数据流分析其实就是在CFG上分析。

绝大部分静态分析都是牺牲了completeness，去追求soundness。放弃了速度，去追求精度。

首先对数据进行抽象，形式化表达；

接下来对程序进行over-approximation，==过拟合==，也就是说程序在运行中所有可能产生的值，都要在静态分析时候去考虑到。

May-Analysis：输出信息可能是正确的，相当于已经做了over-approximation过拟合；

Must-Analysis：输出信息必须是正确的，准确的，相当于已经做了under-approxiamtion欠拟合；

May-Analysis：绝大部分静态分析都是may，会有误报，这是必然

Must-Analysis：会有漏报

一般来说：

May都是union，初始化都是空，bottom

Must都是intersection。初始化是all，top（top就是程序分析中最不准的结果）

三要素：Nodes (BBs/statements)、Edges (control flows)、CFG (a program)

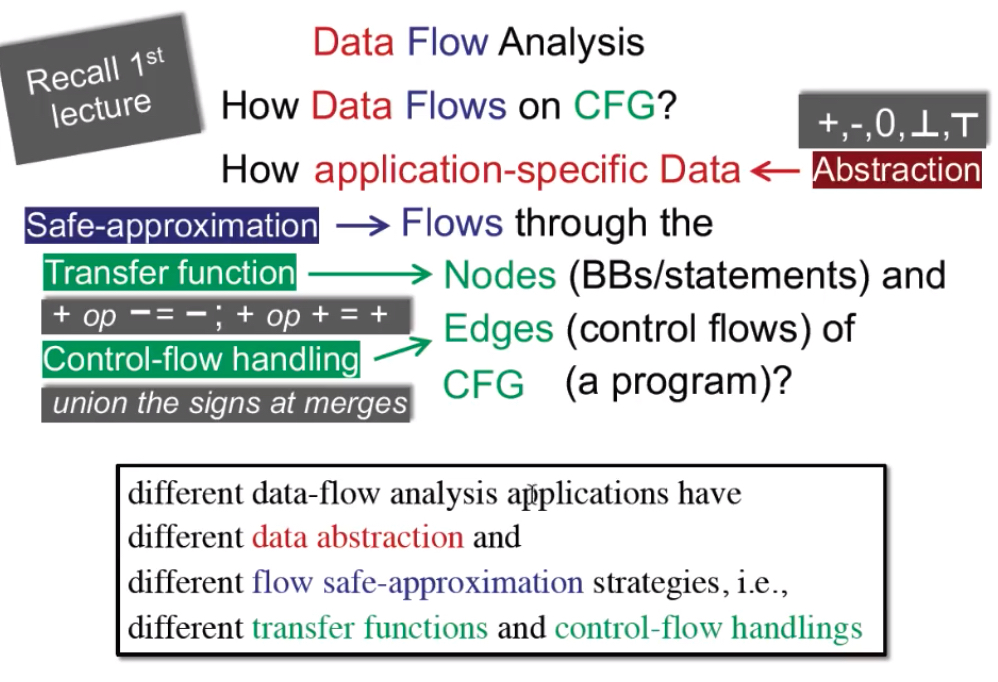
不同的数据流分析 有 不同的数据抽象表达 和 不同的安全近似策略，如 不同的 转换规则 和 控制流处理。

数据流分析预备知识

输入/输出状态：程序执行前/执行后的状态（本质就是抽象表达的数据的状态，如变量的状态）。

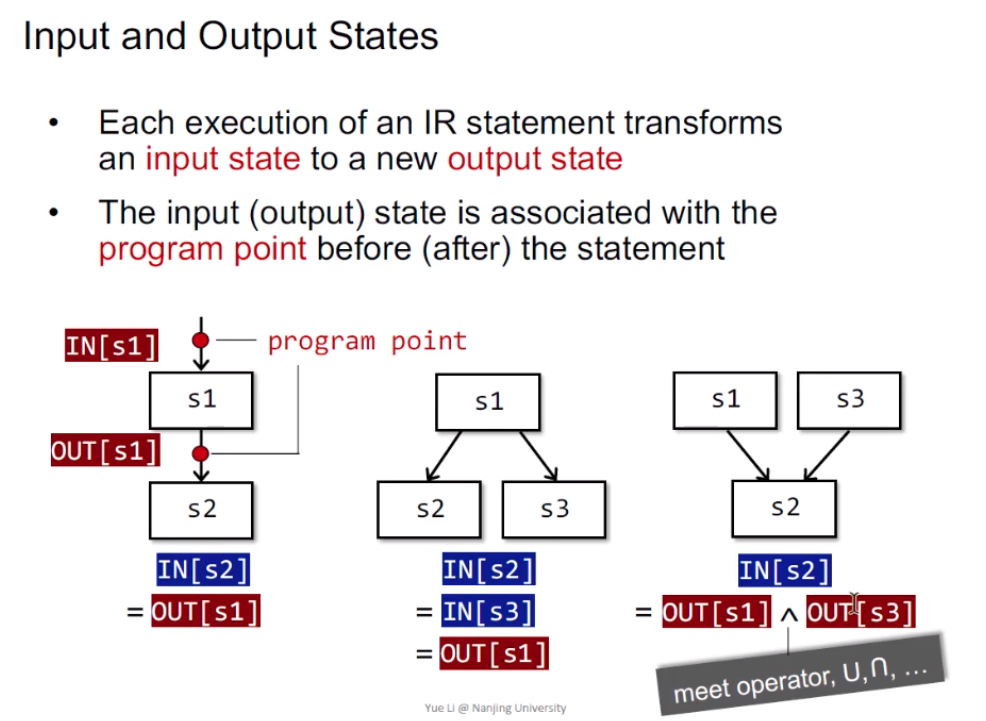
数据流分析的结果：最终得到，每一个程序点对应一个数据流值(data-flow value)，表示该点所有可能程序状态的一个抽象。例如，我只关心x、y的值，我就用抽象来表示x、y所有可能的值的集合（输入/输出的值域/约束），就代表了该程序点的程序状态。

Transfer Funtion：

转换函数，约束规则。

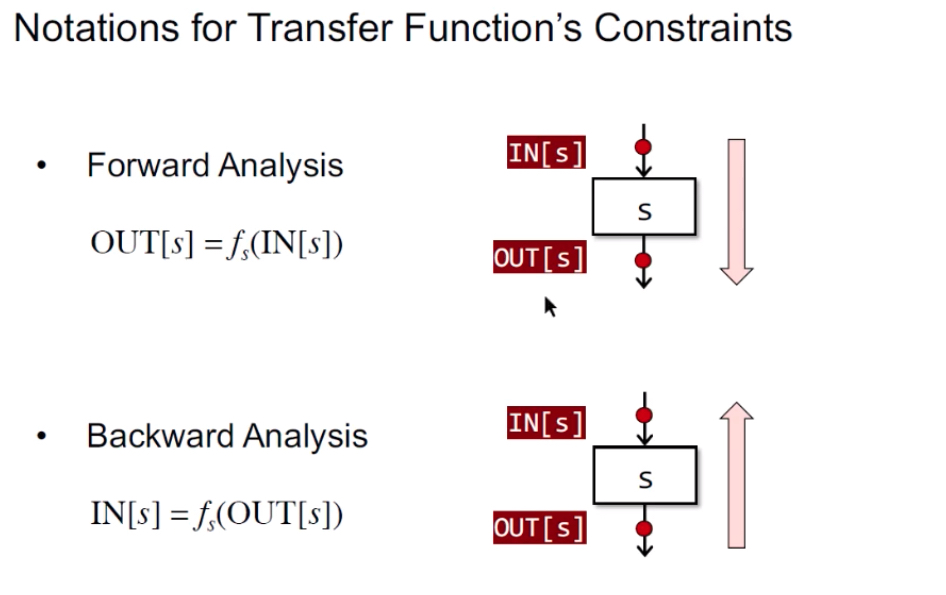
Forward Analysis前向分析：按程序执行顺序的分析。OUT[s]=fs(IN[s])，s-statement
Backward Analysis反向分析：逆向分析。IN[s]=fs(OUT[s])

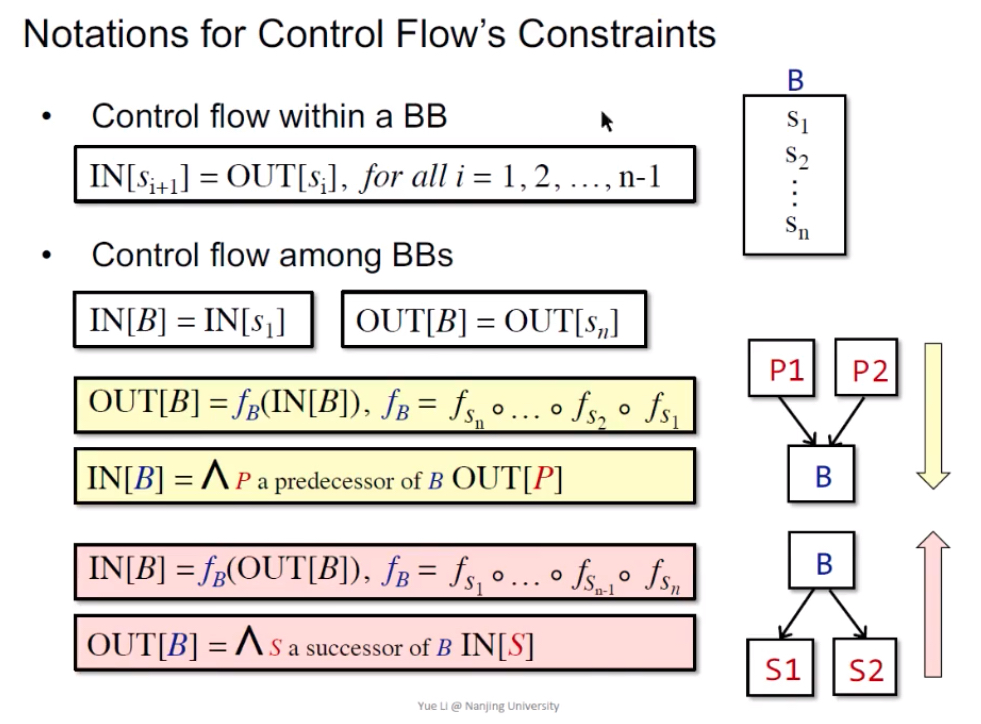
Reaching Definitions Analysis

Forward & MAY

问题定义：在p点给变量v一个定义d（赋值），存在一条路径使得程序点p能够到达q，且在这个过程中v不能被重新赋值。

May：不放过任何一条path，需要over来保证safe

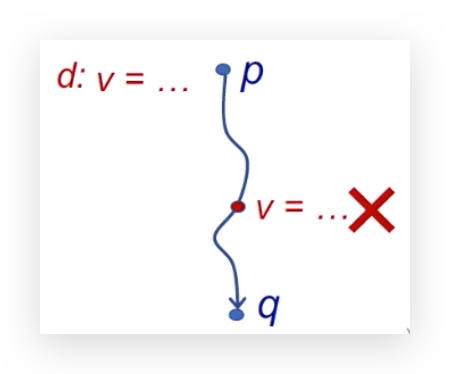
应用举例：检测未定义的变量，若v可达p且v没有被定义，则为未定义的变量。

抽象表示：设程序有n条赋值语句，用n位向量来表示能reach与不能reach。

分析

Transfer Function：OUT[B] = genB U (IN[B] - killB)

解释：基本块B的输出 = B内的所有变量v的定义（赋值/修改）语句 U （基本块B的输入-程序中其它所有定义v的地方）。本质就是本块与前驱修改变量的语句 作用之和（去掉前驱中已经定义的语句）。

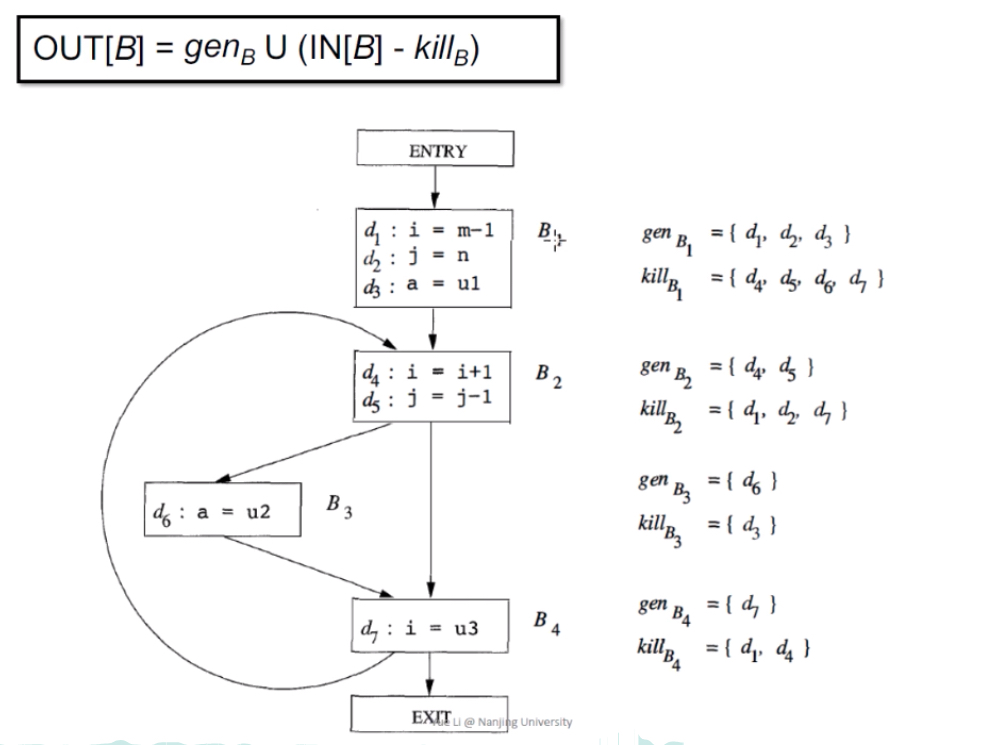
简单例子：

以第一个基本块为例，gen就是d1,d2,d3三个定义语句，kill需要杀掉的就是在d1,d2,d3中定义的变量(i,j,a)在别处也被定义的语句，图里就是d4、d5、d6、d7，他们四个都需要被kill掉。

Control Flow：IN[B] = UNIONp a_predecesso_of_B Out[P] ——怎么理解，就是基于控制流而得到。

解释：基本块B的输入 = 块B所有前驱块P的输出的并集。注意，所有前驱块意味着只要有一条路径能够到达块B，就是它的前驱，包括条件跳转与无条件跳转，所以需要搞并集union。

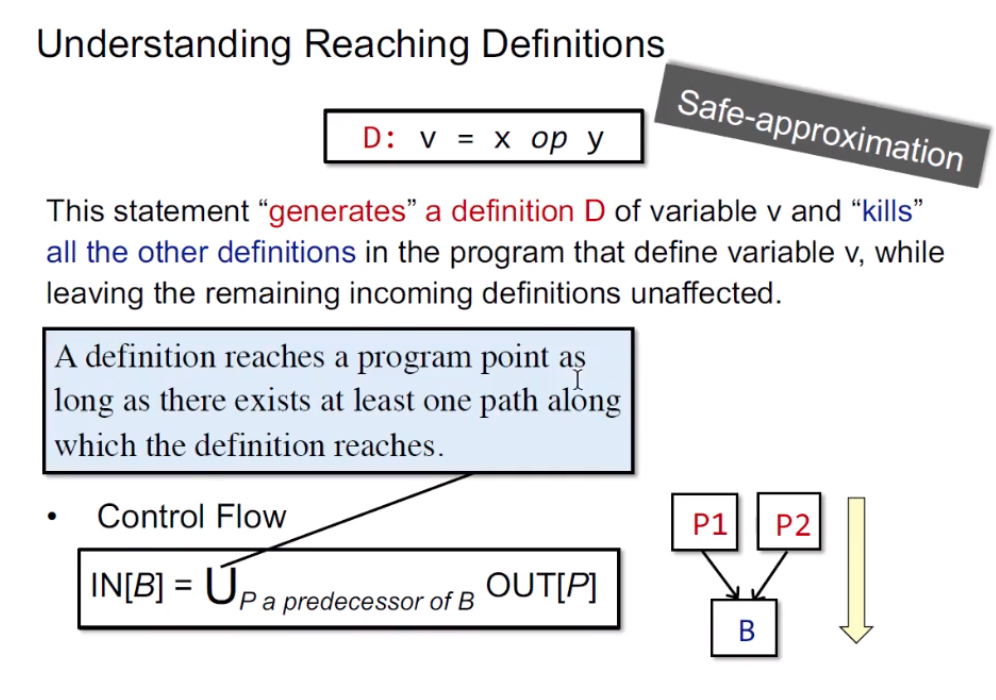
算法

目的：输入CFG，计算好每个基本块的killB（程序中其它块中定义了变量v的语句）和genB（块B内的所有变量v的定义语句），输出每个基本块的IN[B]和OUT[B]。

方法：首先所有基本块的OUT[B]初始化为空。遍历每一个基本块B，按以上两个公式计算块B的IN[B]和OUT[B]，只要这次遍历时有某个块的OUT[B]发生变化，则重新遍历一次（因为程序中有循环存在，只要某块的OUT[B]变了，就意味着后继块的IN[B]变了）。

例子

抽象表示：设程序有n条赋值语句，用n位向量来表示能reach与不能reach。

说明：红色-第1次遍历；蓝色-第2次遍历；绿色-第3次遍历。针对等号左边的变量，先kill，再gen。

结果：3次遍历之后，每个基本块的OUT[B]都不再变化。

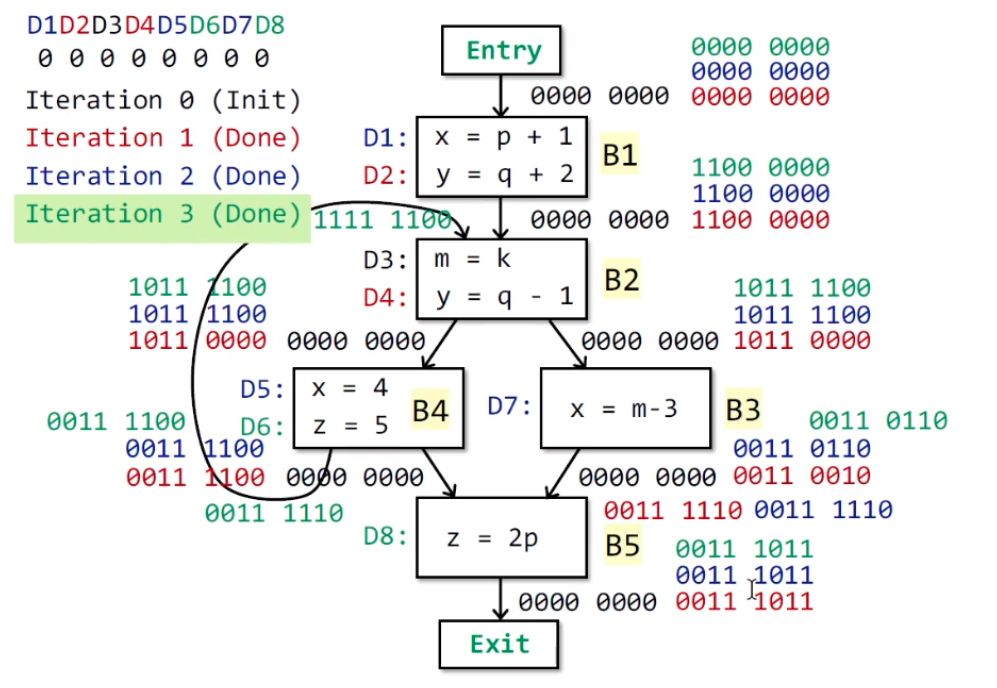
现在，我们可以回想一下，数据流分析的目标是，最后得到了，每个程序点关联一个数据流值（该点所有可能的程序状态的一个抽象表示，也就是这个n位向量）。在这个过程中，对每个基本块，不断利用基于转换规则的语义（也就是transfer functions，构成基本块的语句集）-OUT[B]、控制流的约束-IN[B]，最终得到一个稳定的安全的近似约束集。

停止条件

OUT[B] = genB U (IN[B] - killB)

理解：genB和 killB是不变的，只有IN[B]在变化，所以说OUT[B]只会增加不会减少，程序的定义语句是有限的，所以最终肯定会停止。in决定out，out又决定in。

看下面这张图：

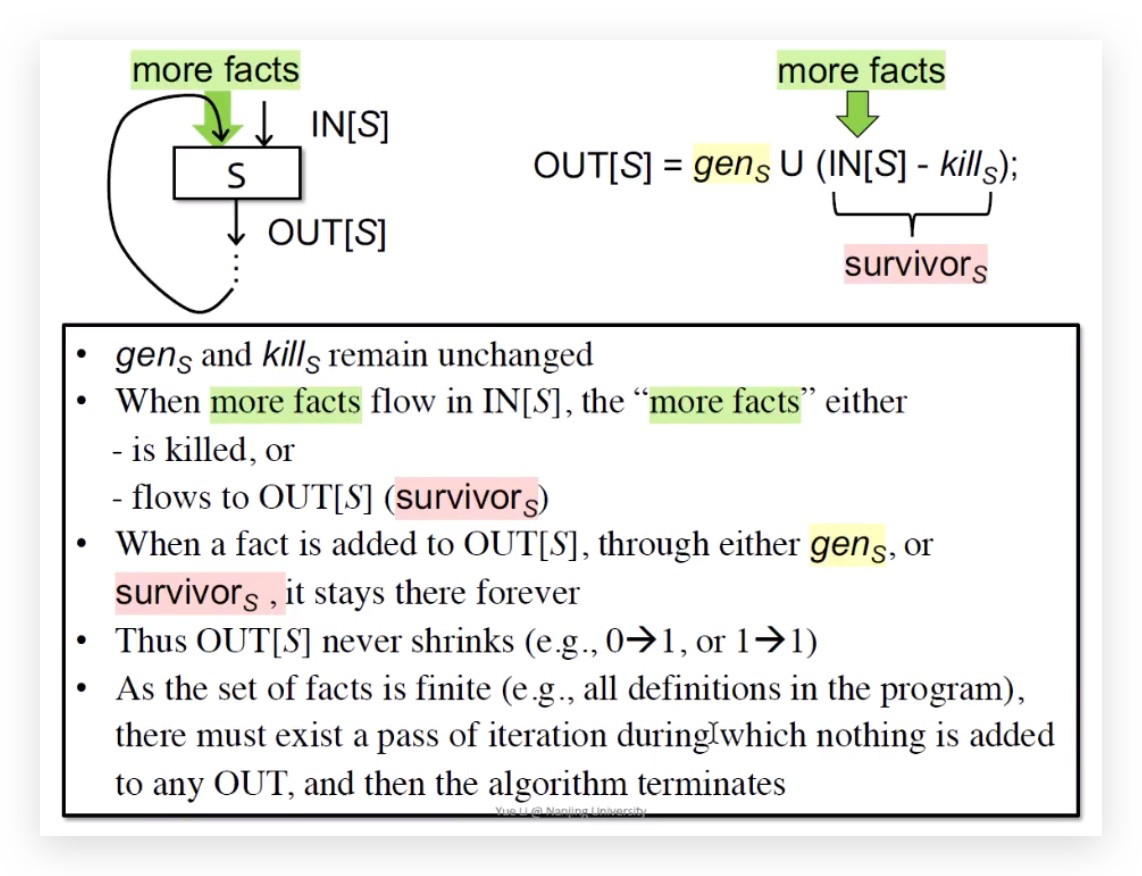
每一次迭代，IN都会加入更多的程序facts，这些facts要么被kill掉、要么成为surviors进入到OUT中。

不论是gen还是surviors，留在OUT中就会一直stay，也就是OUT永远不会缩减。

程序定义点也是有限的，就会导致OUT最终不会变化，算法一定会停止。

04

Live Variables Analysis

Backward & May

问题定义：某程序点p处的变量v，从p开始到exit块的CFG中是否有某条路径用到了v，如果用到了v，则v在p点为live，否则为dead。其中有一个隐含条件，在点p和引用点之间不能重定义v。

应用场景：可用于寄存器分配，如果寄存器满了，就需要替换掉不会被用到的变量。

抽象表示：程序中的n个变量用长度为n bit的向量来表示，对应bit为1，则该变量为live，反之为0则为dead。

分析

Control Flow：OUT[B] = US a_successor_of_BIN[S]

理解：逆向分析，只要有一条path是live，父节点就是live。

Transfer Function：IN[B] = useB U (OUT[B] - defB)

理解：IN[B] = 本块中use出现在define之前的变量 U （OUT[B]出口的live情况 - 本块中出现了define的变量）。define指的是定义/赋值。

IN[B] = useB U (OUT[B] - defB)

IN[B] 其实想看的是哪些变量在进入B之前就已经是live的，那么分为以下两种情况：

第一种是在B中从定义之前就被引用的，useB。

第二种是针对outB来说，逆向分析，如果想知道哪些在进入B之前就是live的，那么就需要从outB中减去那些在B中被重定义的那些，它们就是defB。

两种情况取并集，先killB，再useB。 kill等号左边的local，gen右边的locals。

特例分析：如以下图所示，第4种情况，v=v-1，实际上use出现在define之前，v是使用的。

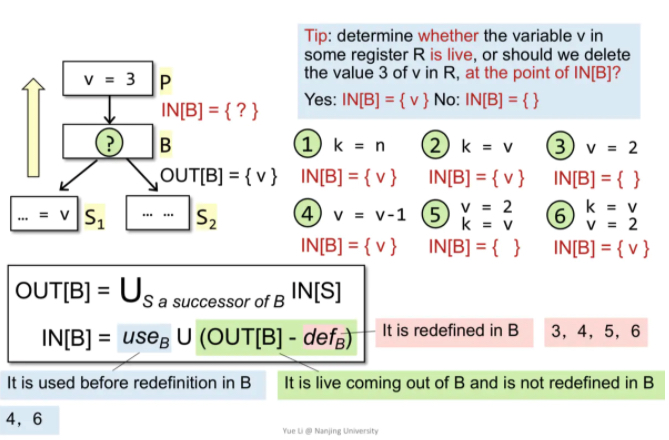
算法

初始化规律：一般情况下，may analysis 全部初始化为空，must analysis全部初始化为all。

目的：输入CFG，计算好每个基本块中的defB（重定义）和useB（出现在重定义之前的使用）。输出每个基本块的IN[B]和OUT[B]。

方法：首先初始化每个基本块的IN[B]为空集。遍历每一个基本块B，按以上两个公式计算块B的OUT[B]和IN[B]，只要这次遍历时有某个块的IN[B]发生变化，则重新遍历一次（因为有循环，只要某块的IN[B]变了，就意味前驱块的OUT[B]变了）。

问题：遍历基本块的顺序有要求吗？ 没有要求，但是会影响遍历的次数。

例子

抽象表示：程序中的n个变量用长度为n bit的向量来表示，对应bit为1，则该变量为live，反之为0则为dead。

说明：从下往上遍历基本块，黑色-初始化；红色-第1次；蓝色-第2次；绿色-第3次。先kill左边的def，再gen右边的use。

结果：3次遍历后，IN[B]不再变化，遍历结束。

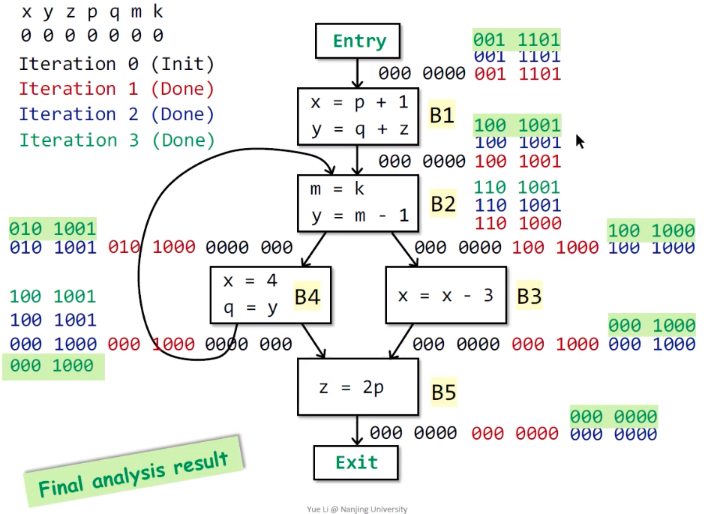
Available Expression Analysis

Forward & MUST

问题定义：

程序点p处的表达式x op y可用需满足2个条件：

1. 从entry到p点的所有路径都必须经过x op y
2. 在最后一次使用x op y之后，没有重定义操作数x、y。（如果重定义了x 或 y，如x = a op2 b，则原来的表达式x op y中的x或y就会被替代）。

应用场景：用于优化，检测全局公共子表达式。

抽象表示：程序中的n个表达式，用长度为n bit的向量来表示，1表示可用，0表示不可用。

分析

Transfer Function：OUT[B] = genB U (IN[B] - killB)

理解：

genB：基本块B中所有新的表达式（并且在这个表达式之后，不能对表达式中出现的变量进行重定义）–>加入到OUT；killB：从IN中删除和被重新定义变量有关的表达式。

Control Flow：

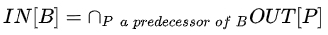
理解：从entry到p点的所有路径都必须经过该表达式。

问题：该分析为什么属于must analysis呢？因为我们允许有漏报，不能有误报，比如以上示例中，改为x=3，去掉 b=e16*x，该公式会把该表达式识别为不可用。但事实是可用的，因为把x=3替换到表达式中并不影响该表达式的形式。这里虽然漏报了，但是不影响程序分析结果的正确性。

算法

目的：输入CFG，提前计算好genB和killB。

方法：首先将OUT[entry]初始化为空，所有基本块的OUT[B]初始化为1…1。遍历每一个基本块B，按以上两个公式计算块B的IN[B]和OUT[B]，只要这次遍历时有某个块的OUT[B]发生变化，则重新遍历一次（因为有循环，只要某块的OUT[B]变了，就意味后继块的IN[B]变了）。

例子

抽象表示：程序中的n个表达式，用长度为n bit的向量来表示，1表示可用，0表示不可用。

说明：黑色-初始化；红色-第1次；蓝色-第2次。先kill再gen。kill看等式左边的local，gen看等式右边的expr。

结果：2次遍历后，OUT[B]不再变化，遍历结束。

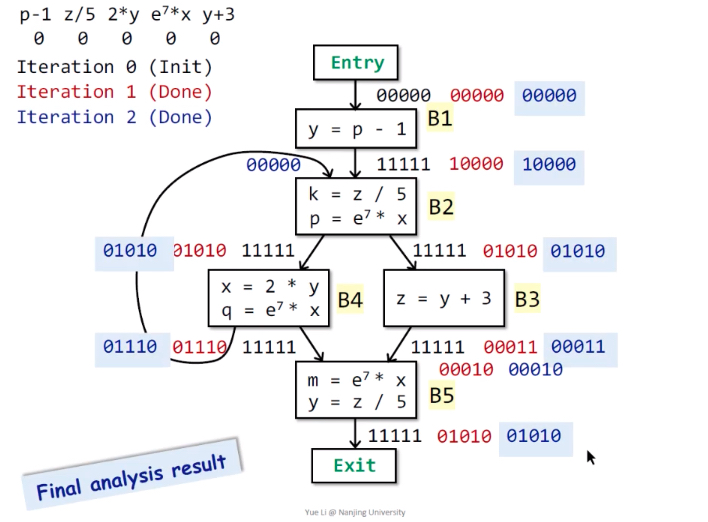
三种分析方法对比

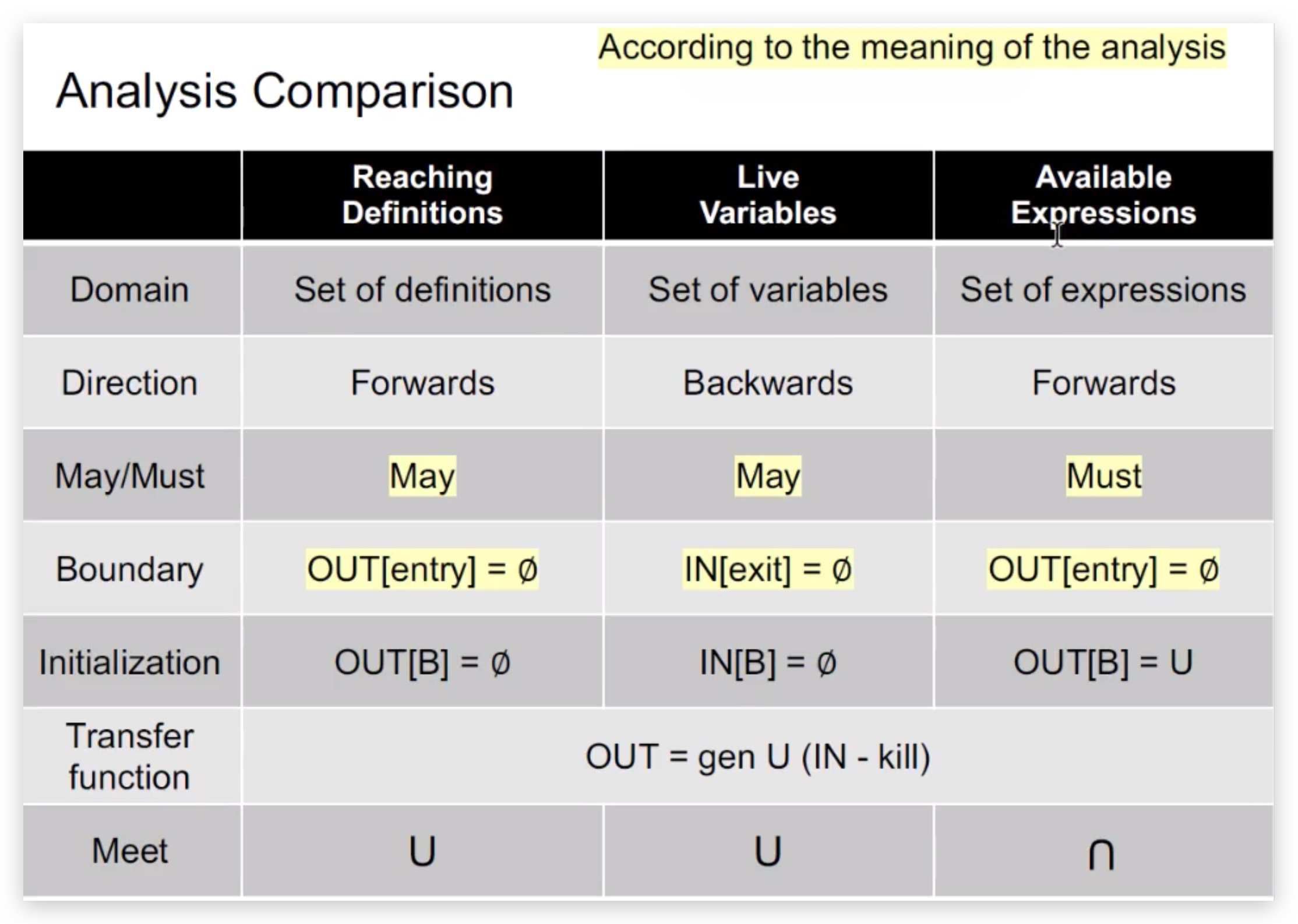
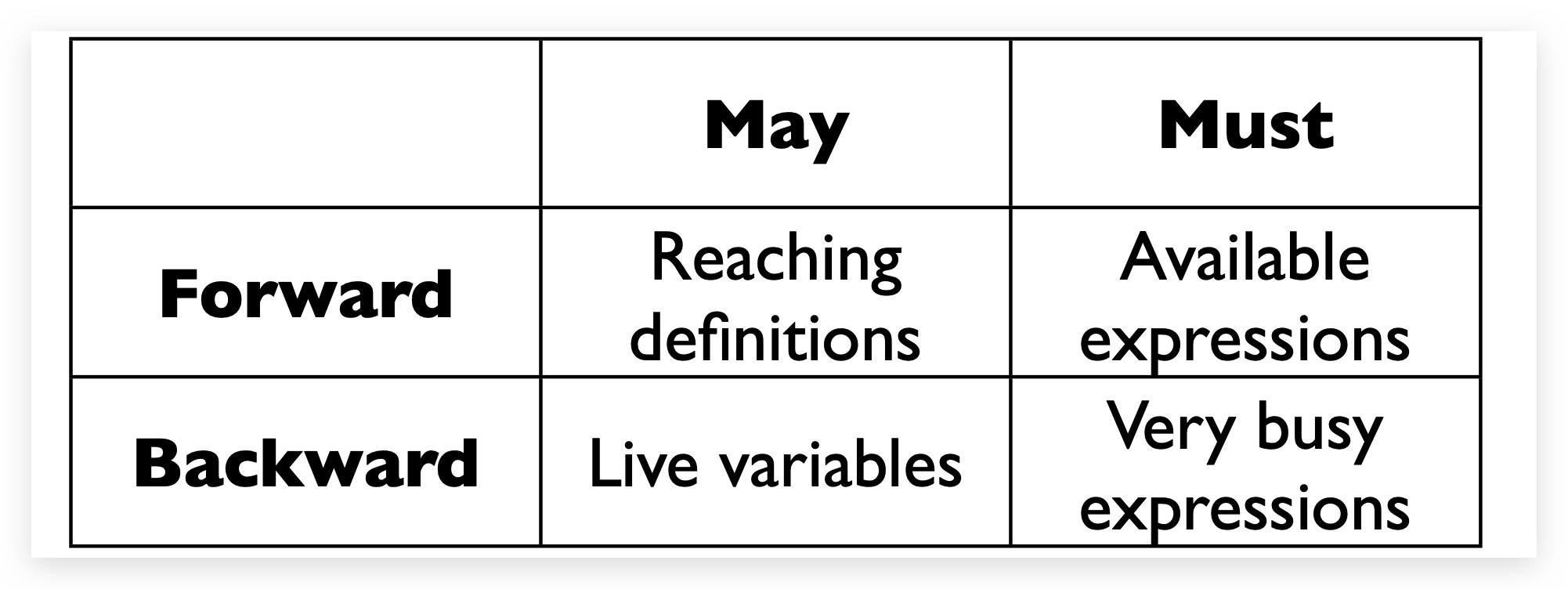
问题：怎样判断是May还是Must？

Reaching Definitions表示只要从赋值语句到点p存在1条路径，则为reaching，结果不一定正确；

Live Variables表示只要从点p到Exit存在1条路径使用了变量v，则为live，结果不一定正确；

Available Expressions表示从Entry到点p的每一条路径都经过了该表达式，则为available，结果肯定正确。

05 & 06

迭代算法实质分析

理论

本质：常见的数据流迭代算法，目的是通过迭代计算，最终得到一个稳定的不变的解。

图示

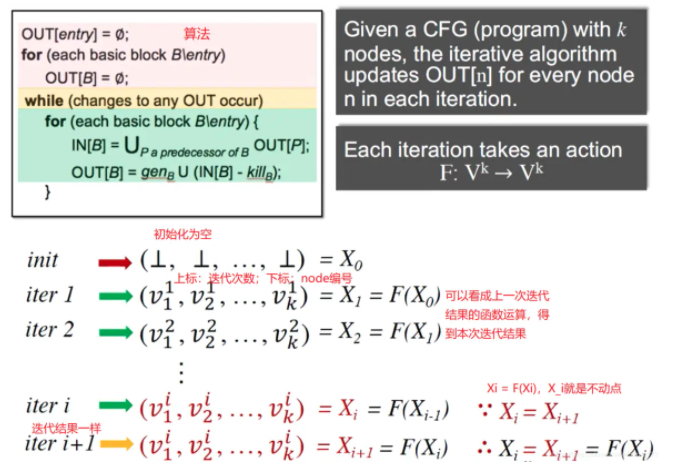
不动点：当Xi = F(Xi)时，就是不动点。

问题：

• 迭代算法是否一定会停止（到达不动点）？
• 迭代算法如果会终止，会得到几个解（几个不动点）？
• 迭代几次会得到解（到达不动点）？

偏序 Partial Order

上下界 Upper and Lower Bounds

定义

理解：

S是P的子集，

如果S中所有元素x，都有x≤u，那么就称u是子集S的上界。u属于P，但是u并不一定在S中。

如果S中所有元素x，都有i≤x，那么就称i是子集S的下界。i属于P。

最小上界：lub，上界里最小的那个；

最大下界：glb，下界里最大的那个；

实例

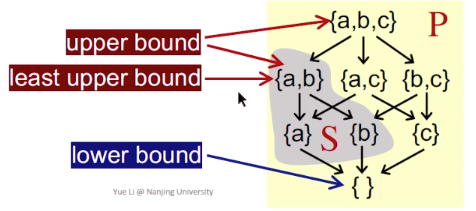
特性

并非每个偏序集都有上下确界。

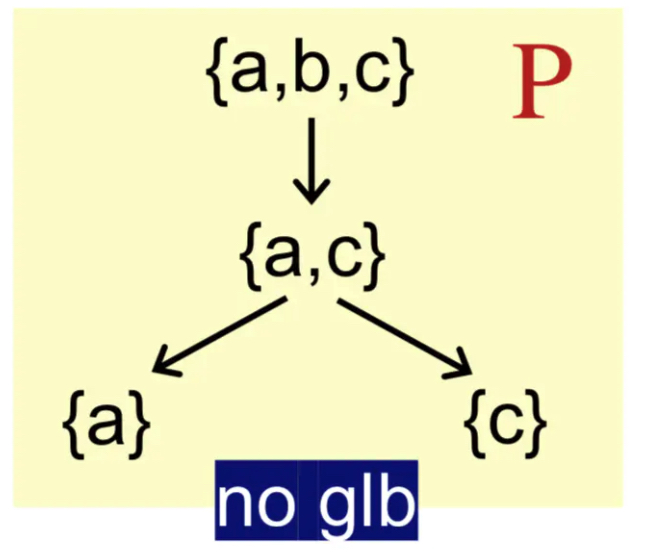
如果存在上下确界，则是唯一的。unique

利用传递性和反证法即可证明。

Lattice 格论

格

理解：

任意两个元素构成的集合都存在最大下界和最小上界，那么这个偏序集就是格。

join union 最小上界

meet intersection 最大下界

半格

全格

理解：

finite -> complete 但是complete不能保证是finite的

全格，任意子集都有最大上界和最小下界。

格点积

数据流分析框架 via.Lattice

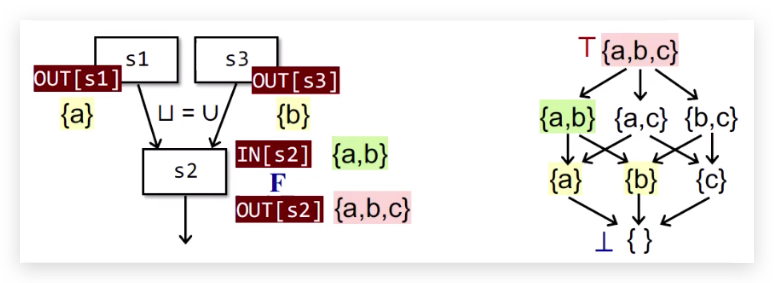
单调性与不动点定理（Monotonicity&Fixed Point Theorem）

证明：

理解：

迭代算法转换到不动点理论

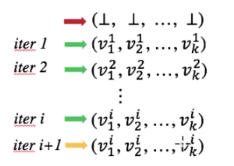
说点自己的理解：

单调性：

transfer function ： gen & kill 保证了never shrinks 所以是单调的

join&meet :

第三个问题：

算法何时能够达到不动点？

Lattice高度：是lattice上从top到bottom之间最长的路径。

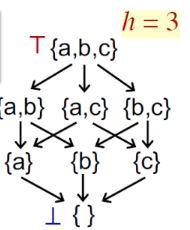
最差的迭代次数：

h x k

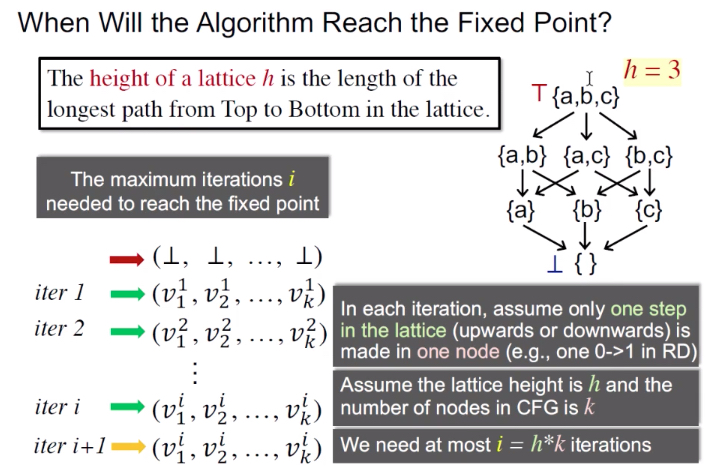
迭代次数最差情况：

每个BB的OUT/IN值只变化一个（0->1）

最坏的情况就是lattice上每次只走一步，每一步只改一个bit位置

图中lattice的高度是h ( h = 3 )，一共k个node，每一轮都需要走h步，每个node只改一个，那么当然就需要h x k次

从Lattice角度看may/must分析

根据如下的图，逐步讲解整个过程：

需要记住的前提：

不论是may-analysis和must-analysis都是从不安全（unsafe result）到安全（safe result）

并且，may-analysis和must-analysis都是从准确（precise）到不准确（un-precise）

注意：现在是在对may/must analysis的算法整体流程分析，从lattice的角度。但是本身该算法是safe的——这是由safe-approximate来保证的，而不是通过lattice或者其他保证的。

May analysis

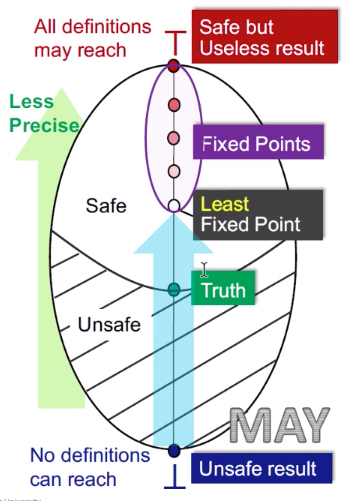
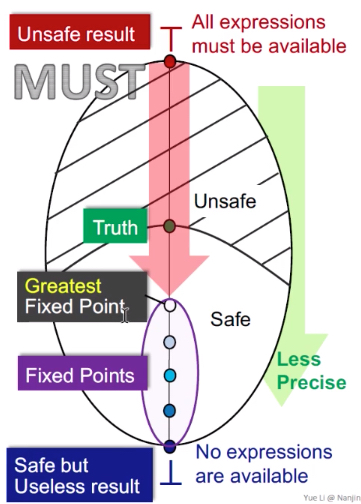
• 从bottom开始，bottom代表的是所有定义都是可达的——这就是不安全的结果（因为验证本质上是一个查错的工具，现在的验证结果是没有任何一个错误，这就是不可靠的）

• 图中的no definitions can reach这个是根据可达性定义的应用来考虑的。可达性定义会应用在变量是否初始化中，它会在entry给每个变量一个UNDEF(图里的definitions只是个形式化表达)，这里的意思就是指所有的UNDEF都无法到达，那么就意味着程序中会将每个变量都初始化——那么就是该程序无未初始化错误——分析的结果是不安全的

• 最上面到top，top代表的是所有定义都是不可达的——从查错角度来讲，这句话是安全的，因为所有定义都有可能存在错误，但是这句话没有用——程序未验证前，就可以说这句话了——所以是safe but useless

• 图中的all definition may reach就是指，可达性定义应用中的那些个UNDEF，都是可达的，那么所有变量都是未初始化的——所有变量都可能存在未初始化的错误——分析的结果是安全的，但是是个废话

• 中间的truth：

  表明最准确的验证结果，假设{a,c}是truth，那么包括其以上的都是safe的，一下的都是unsafe，就是上图的阴影和非阴影。

  

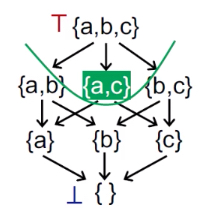
• 并且都是从不安全到安全的过程——所以箭头从下向上

• 从bottom开始，得到的是最小不动点，就是离truth最近的，是最准确的。 向上还有多个不动点，但是准确度越来越不准（直到top就是最不准的）——bottom都是000000，top都是111111，may analysis得到的解是最小不动点，就是最优解，是最准的那一个。

  ——所以，可达定义得到的是最准确的结果，虽然还是soundness的（过近似）

Must analysis

前向分析，从上往下，但还是从unsafe到safe。

must analysis以available表达式为例。

• 从top开始，代表所有表达式都是可用的——是最unsafe的——top是1111111
• 如果是利用在表达式计算优化中，那就是有很多已经被重新定义的表达式也被优化了（实际上不能被优化）——那么该优化就是错误的
• 到bottom，代表没有表达式是可用的——是安全的，但是是无用的
• 从top开始到bottom，就是unsafe到safe的转变，存在一个truth，代表程序真实的结果；
• 分析从top到bottom，达到的就是最大不动点，离truth最近，那么该最大不动点得到的解就是最优的——must analysis得到的解是最大不动点，就是最优解–为什么是最大不动点，tricky一下，最上面都是11111，最下面都是00000，是一个递减的过程，得到的第一个不动点当然是最大不动点

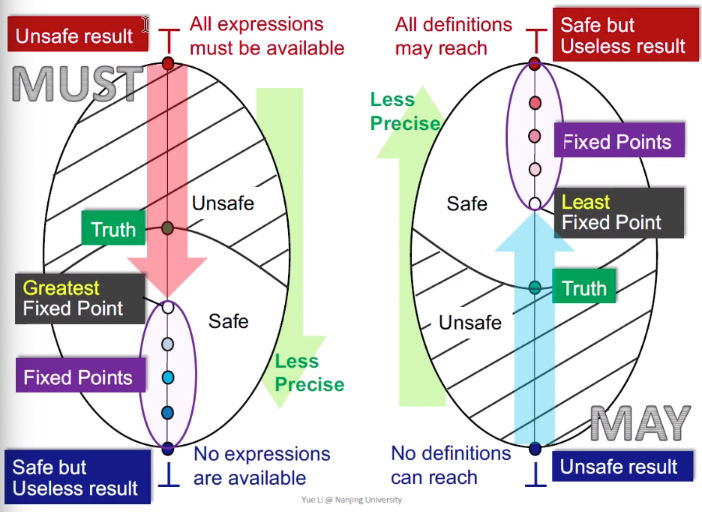
战术“多讲几句”：

tranfer function和control flow

前者是写死的，control flow里面有join还是meet决定了很多

比如说000和001去join，是001，其实join就是获得了最小上界lub而不是一大步直接迈到111(111是上界 但不是lub)，每次也都是迈出了最小的一步，minimal step。

MOP & Distributivity

MOP: Meet-over-all-paths solution

将所有路径都join/meet的方法，通常用来衡量精度。

这里的meet是统称meet和join两种合并操作。

区别

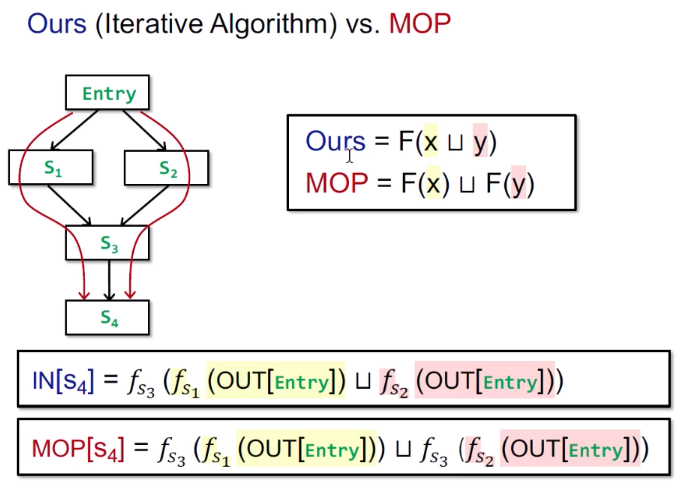
理解：

这里其实都是在追求一种近似解，求解近似解的方法中最基本的一个就是对问题进行抽象。

引入两个近似方案：

1. 忽略所有路径的条件判断，认为所有分支都是可达的。
2. MOP or Distribute
   1. Distribute：结合transfer function，也就是gen-kill问题。gen-kill这种数据流方程的做法其实是在汇聚点的位置提前做合并。
   2. MOP：遍历所有可能的路径并且在路径的尾部进行数据流结果的合并。

Worklist算法

是迭代算法的一种优化，更常用

本质：就是只将有变化的值挑出来，再去利用转换函数和控制流操作。

07

Motivation

过程内分析：Intra-procedual Analysis，未考虑函数调用，导致分析不精确。

过程间分析：Inter-procedural Analysis，考虑函数调用，又称为全程序分析（Whole Program Analysis），需要构建调用图call graph，加入Call edges和Return edges。

Call Graph 调用图

调用图定义

定义：本质是调用边的集合，从调用点（call-sites）到目标函数（target methods / callees）的边。

应用：是所有过程间分析（跨函数分析）的基础，程序优化，程序理解，程序调试。

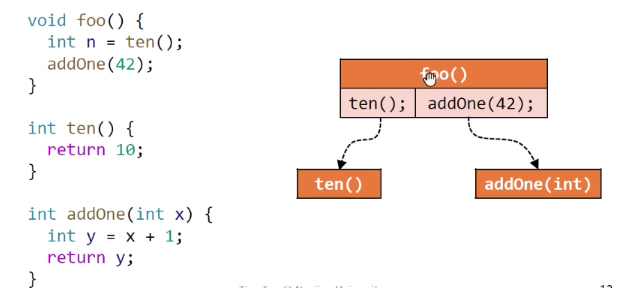
面向对象语言OOL的调用图构造 Java

代表性算法：从上往下精度变高，速度变慢，重点分析第1、4个算法。

• Class hierarchy analysis(CHA)
• Rapid type analysis(RTA)
• Variable type analysis(VTA)
• Pointer analysis(k-CFA)

Java调用分类：

	Static call	Special call	Virtual call
指令	invokestatic	invokespecial	invokeinterface、 invokevirtual
Receiver objects	×	✓	✓
目标函数	Static函数	构造函数、 私有函数、父类的实例函数	其他实例函数
目标函数个数	1	1	≥1 (polymorphism多态性)
何时确定	编译时	编译时	运行时

理解：

一个virtual call 在程序运行的不同状态时，可能调用到不同的目标方法，具有多态性，运行时确定。

Virtual call 是 构造调用图的实际关键所在。

virtual call在程序运行时才能得到，基于2个要素得到：

1. reciever object的具体类型：c

2. 调用点的函数签名：m。（通过signature可以唯一确定一个函数）Soot采取的格式

   1. signature = 函数所在的类 + 函数名 + 描述符
   2. 描述符 = 返回类型 + 参数类型

   简记为C.foo(P, Q, R)

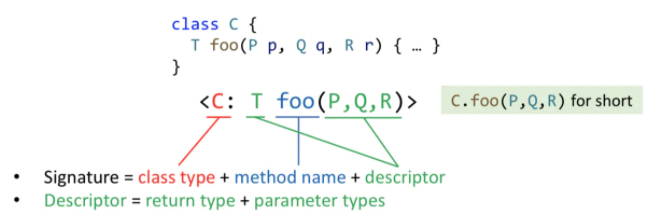
Method Dispatch（Virtual call）

定义：用Dispatch(c, m)来模拟动态Method Dispatch过程，c表示reciever object，m表示函数签名。

解释：若该类的非抽象方法（实际可执行的函数主体）中包含和m相同名字、传递/返回参数的m‘，则直接返回；否则到c的父类中找。

示例：

理解：

Dispatch（B,A.foo()）先对B类自己进行，但是B没有foo方法，向上找父类A才有。

Dispatch（C,A.foo()）C自己本身就有，那么就是C自己的方法。

Class Hierarchy Analysis CHA 类层次分析

目的：根据每个virtual call 的 receiver varible 的声明类型来求解所有可能调用的目标函数。如 A a = ... ; a.foo(); 这个a就是receiver object，声明类型就是A。

CHA假定a可以指向A以及 A所有子类对象，CHA的过程就是从A和子类中去找目标函数。

算法：Resolve(cs)——利用CHA算法找到调用点所有可能的调用目标。

示例：

算法应用：

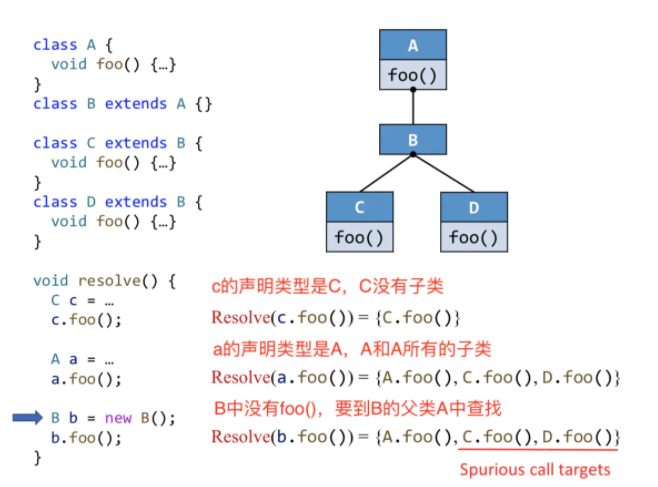
理解：

第三个b.foo（）

算法里面说是对b和b的所有子类进行dispatch：

1. b自己：没有 向上找父类 父类是A 那么就是A.foo()
2. b所有子类：C和D 那么就是C.foo()和D.foo()

以上b.foo()的调用目标 C.foo()和D.foo()是错误，理论上是假的，因为已经指定了是B类型，所以b.foo()根本不会调用C、D的foo()。因为CHA只考虑声明类型，也就是B，导致准确度下降。多态性就是说，父类可以引用子类的对象，如B b=new C()。

优缺点：CHA优点是速度快，只考虑声明类型，忽略数据流和控制流；缺点是准确度低。

总结：本类中有同名函数就在本类和子类找，没有就从父类找，接着找父类的子类中的同名函数（CHA分析）。

利用CHA生成整个程序的调用图

思想：遍历每个函数中的每个调用指令，调用CHA的Resolve()找到对应的目标函数和调用边，函数+调用边=调用图。

步骤：

1. 从main方法开始，作为入口方法。
2. 对于每个可达方法m，求Resolve（cs）。
3. 不断重复，直到没有新的方法，全遍历。

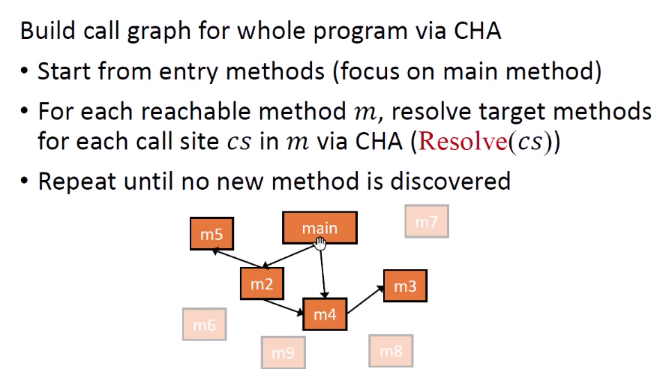
算法：

m_entry=程序的入口方法

示例：

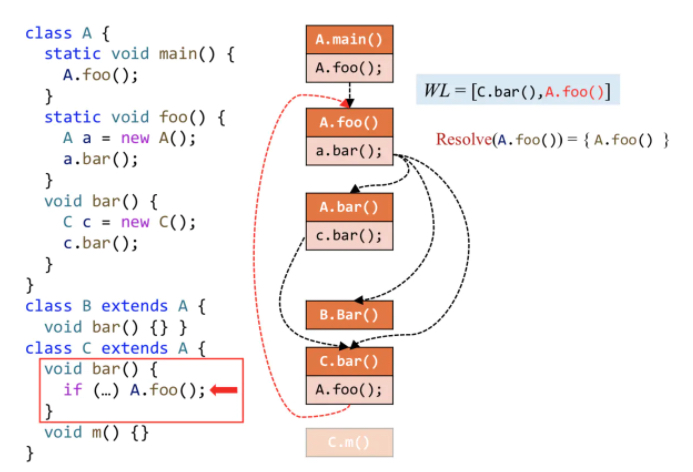
理解：

首先WL集合就是待处理方法，一开始WL里面就是A.main()。

浅色块是call site，深色块是自己类中的方法。

首先把main方法取出来，Resolve解它，是静态方法，只有他自己，那么连上一条调用边，目标方法A.foo()加入到WL中。

接着处理A.foo()方法，它里面有一个new a.bar()，那么a.bar()的目标方法就是A，B，C三个bar方法，三条边，并且这三个方法都加入到worklist里面。

再取A.bar()，它的目标方法就是C.bar()，也要正常加入WL里面。

接着是B.bar()，那么就是啥也不做。

最后一个是C.bar()，同样调用A.foo()，加边。

跳过最后的C.foo，A.foo。

过程间控制流分析图 Interprocedural Control-Flow Graph ICFG

定义：过程间控制流图ICFG = 各个方法自己的CFG + (Call edges + Return edges)。

• Call edges：连接调用点和目标函数入口
• Return edges：从return语句连到Return site（Call site后面一条语句）

说明：对ICFG进行数据流分析，目前没有标准的一套算法。

对比：

	Intraprocedural	Interprocecdural
程序表示	CFG	ICFG = CFGs + call & return edges
转换规则	Node transfer	Node transfer + edge transfer

常量传播数据流分析：

• Node transfer：与过程内分析相同，对每个调用点，将等号左边kill掉。
• Call edge transfer：传参
• Return edge transfer：传返回值

常量传播示例：

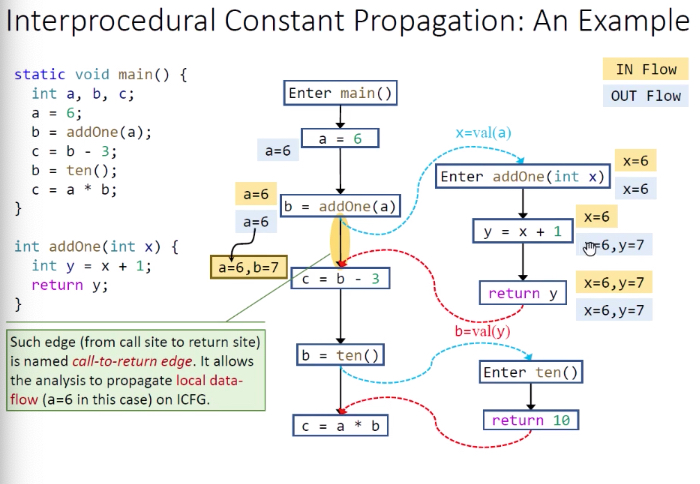
理解：

首先也是从main方法开始，黄色代表in-flow，蓝色代表out-flow。

call的时候kill掉左手边变量，直接flow过去，就算有值也是return过来的。

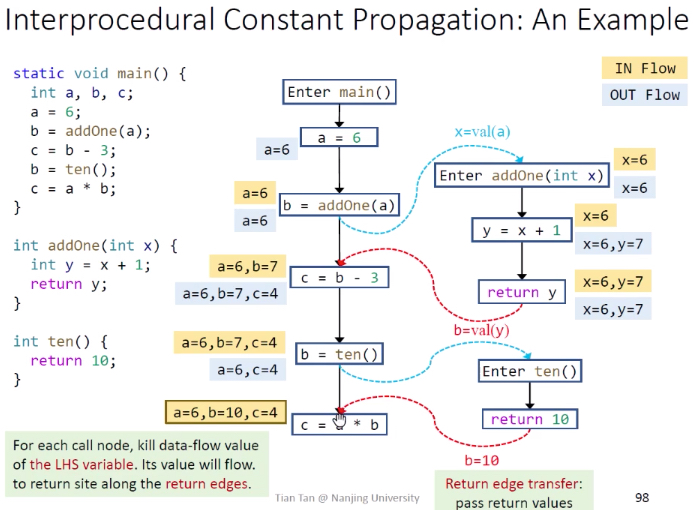
说明：黄色背景边必须有，从b = addOne(a)到c=b-3，a通过此边传递，b通过addOne()传递。若a也通过addOne()传递，会额外消耗系统资源。

在倒数第二个

b = ten();

需要把b在flowset中kill掉，因为b的值会在返回值里面被改掉

08 & 09

终于来到了指针分析

指针分析必要性：

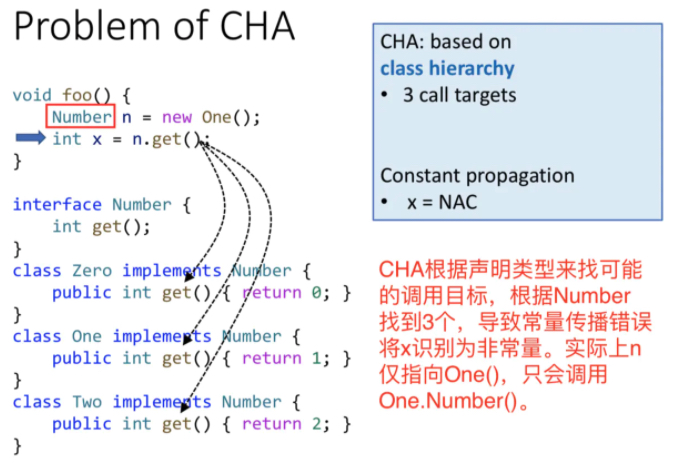
指针分析

目标：分析程序指针可以指向哪些内存区域。对于Java等面向对象语言，主要分析指针指向哪个对象。

说明：指针分析属于may analysis，分析的结果是某指针所有可能指向哪些对象Object，是个over-approximation集合。

示例：面向对象语言中的指针指向问题。对于setB()函数，this指向new A()，因为是调用者是a.setB()；setB()中的b是x传过来的，所以b指向new B()，A.b指向 new B()。

区别：

• 指针分析：分析指针所有可能指向的对象。
• 别名分析：分析两个指针是否指向相同的对象，可通过指针分析来推导得到。如果指向同一个对象，那么就是别名关系。

应用：基本信息（别名分析/调用图），编译优化（嵌入虚拟调用），漏洞（空指针），安全分析（信息流）。

指针分析影响因素

指标：精度（precision）& 效率（efficiency）。

影响因素：本课程，我们主要分析分配点的堆抽象技术、上下文敏感/不敏感、流不敏感、全程序分析。

因素	问题	选项
Heap abstraction	如何建模堆内存？	• Allocation-site • Storeless
Context sensitivity	如何建模调用上下文？	• Context-sensitive • Context-insensitive
Flow sensitivity	如何建模控制流？	• Flow-sensitive • Flow-insensitive
Analysis scope	分析哪部分程序？	• Whole-program • Demand-driven

写在前面

指针分析中往往会遇到flow-sensitive、path-sensitive、context-sensitive

• flow-sensitive：关注语句的顺序。比如说在流敏感的指针分析中，一个非流敏感指针别名分析可能得出“变量x和y可能会指向同一位置”，而流敏感指针别名分析得出的结论类似于“在执行第20条指令后，变量x和y可能会指向同一位置” 。所以，一个非流敏感指针别名分析不考虑控制流，并认为所发现的别名在程序所有位置均成立。
• path-sensitive：关注程序控制流的分支。路径敏感往往会导致“路径爆炸“(path explosion)，“无限搜索空间”(infinite search space)
• context-sensitive：*关注过程间分析，考虑函数调用的上下文关系。 *

堆抽象 Allocation Site（内存建模）

问题：程序动态执行时，堆对象个数理论上是无穷无尽的，但静态分析无法处理这个问题。所以为保证指针分析可以终止，我们采用堆抽象技术，将无穷的具体对象抽象成有限的抽象对象。也就是，将有共性的对象抽象成1个静态对象，从而限制静态分析对象的个数。

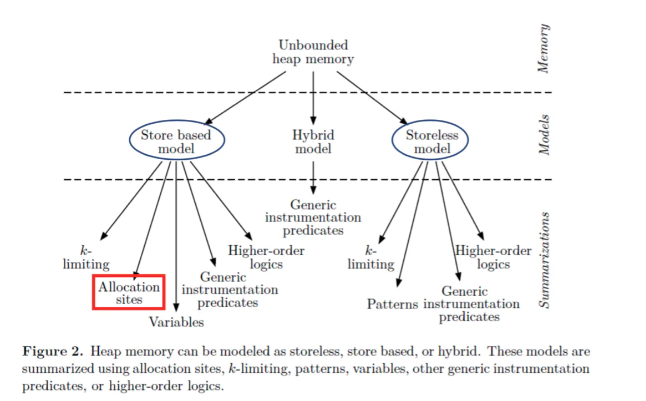
我们只学习Allocation-Site技术，最常见也最常被使用。

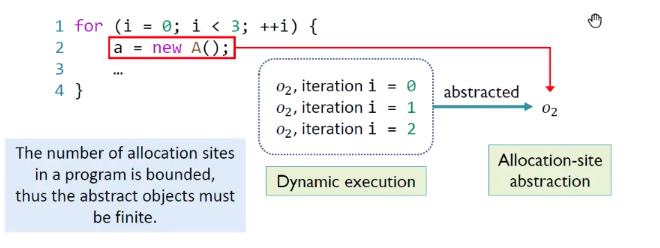
Allocation-Site原理：将动态对象抽象成它们的创建点（Allocation-Site），来表示在该点创建的所有动态对象。Allocation-Site个数是有限的。

示例：循环创建了3个对象，我们用O2来抽象表示这3个动态对象。几个new就会合并处理几个。

上下文敏感Context Sensitivity

问题：考虑是否区分不同call-site对同一函数的调用。

• Context-sensitive：根据某函数调用上下文的不同，多次分析同一函数，更加准确。
• Context-insensitive：将不同的上下文merge到一起，每个函数只分析一次。

流敏感 Flow Sensitivity 控制流建模

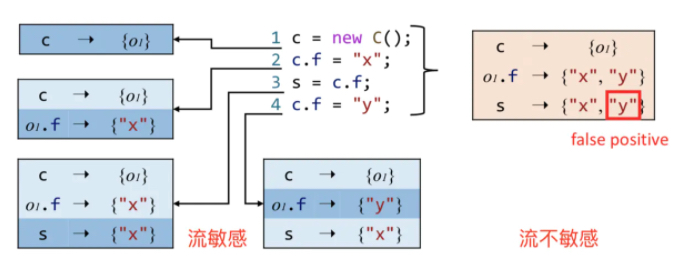
问题：考虑语句顺序（控制流）的影响 vs 把程序当做无序语句的集合。

方法：流敏感会在每个程序点都保存一份指针指向关系映射表，而流不敏感则对整个程序只保存一份指向关系映射。

说明：目前流敏感对Java提升不大，不过在C中很有效，本课程分析的是Java，所以Java重点讨论流不敏感技术。

指针分析示例：

分析范围 Analysis Scope

问题：分析程序的哪一部分？

• Whole-program 全程序：分析全程序的指向关系。
• Demand-driven 需求驱动：只分析影响特定域的指针的指向关系。会很耗费资源。

分析语句种类

问题：哪些语句会影响指针指向，那就只分析这些语句。

Java指针类型：

1. Lacal variable: x
2. Static field:C.f （有时称为全局变量）——不分析
3. Instance field: x.f 对象的field 把他们的组合看成是一个pointer object
4. Array element: array[i] ——不分析，因为静态分析无法确定下标，所以将array中所有成员映射到一个field中，等价于Instance field，所以不重复分析。如下图所示：

五个影响指针指向的语句：

1. New: x = new T()
2. Assign：x = y
3. Store： x.f = y
4. Load： y = x.f
5. Call： r = x.k(a,…)
   • Static call： C.foo()
   • Special call： super.foo() / x.<init>() / this.privateFoo()
   • Virtual call：x.foo() 重点分析

指针分析规则

首先分析前4种语句：New / Assign / Store / Load。

指针分析的域和相应的记法：变量/函数/对象/实例域/指针，用pt表示程序中的指向关系（映射）。

理解：

指针Pointers，指的就是两部分：

1. 程序内部所有变量V
2. 实例对象的属性域O X F

这里面P(O)指的是对象的幂集；

pt(p)表示p点的指针集。

这里可以把Points-to relations理解为Map就是映射，Key就是指针，Value就是指针指针集。

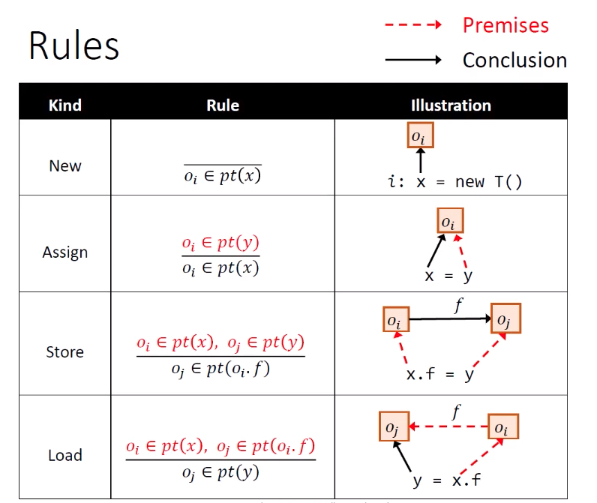
规则：采用推导形式，横线上面是条件，横线下面是结论。

• New：创建对象，将new T()对应的对象oi加入到x的指针集。
• Assign：将y的指针集加入到x对应的指针集。
• Store：让oi的field指向oj。
• Load：Store的反操作。

指针分析实现方式

算法要求：全程序指针分析，要容易理解和实现。

本质：在指针（变量/域）之间传递指向信息。Andersen-style分析（很普遍）——很多solving system把指针分析看作是一种包含关系，eg，x = y，x包含y。

问题：当一个指针的指向集发生变化，必须更新与它相关的其他指针。如何表示这种传递关系？答案PFG。

PFG：用指针流图PFG来表示指针之间的关系，PFG是有向图。

• Nodes：Pointer = V U (O x F) 节点n表示一个变量或抽象对象的域。
• Edges：Pointer X Pointer 边x -> y 表示指针x指向的对象may会流入指针y。

Edges添加规则：根据程序语句 + 对应的规则。

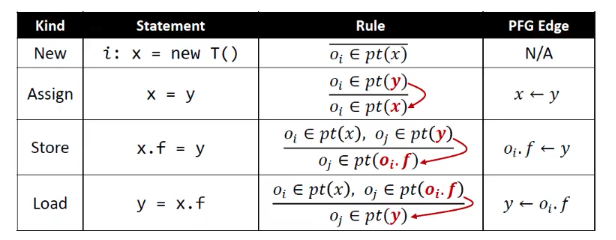
示例：

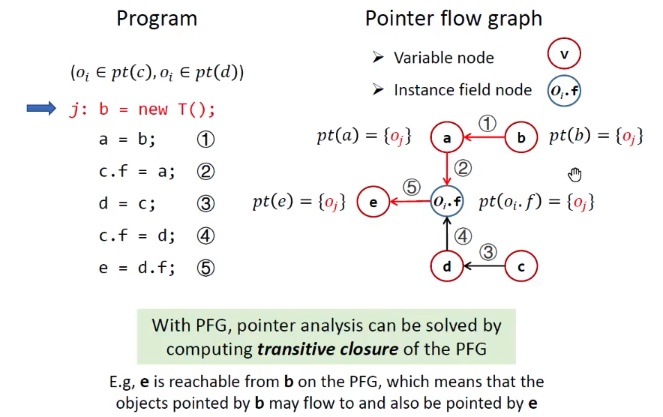
指针分析PTA方法：

1. 构造PFG，PFG也受指向关系的影响。
2. 根据PFG传播指向信息。

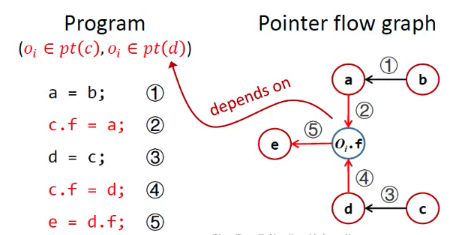
指针分析算法

过程内PTA算法

符号：

• S：程序语句的集合。
• WL：Work list，待合并的指针信息，二元组的集合，<指针n，指向的对象集合pts>，代表的是pts将被加入到n的指向集pt(n)中。
• PFG：指针流图，边的集合。

addEdge做了什么呢？

首先如果s->t这条边在PFG中不存在，那么加一条s->t的边，如果s自身指针集里面还有东西，那么需要向WL中添加<t,pts>，也就是说s自身指向的所有东西，现在都需要被t指向。

换句话说，pts流向了t

Propagate做了什么呢？Propagate(n,delta)

首先 如果delta不为空，那么需要更新ptn，向ptn中增加delta

接下来，对于PFG中，n的后继们，delta需要加入到他们每一个人的指针集里面

理解：

WL <a,ptb>表示是ptb需要加入到a指针集里面 是一种TODO

AddEdge(s,t)

如果s->t在PFG中没有出现过，那么就添加到PFG之中

如果s的指针集非空，那么就向WL中添加<t,pts>

表示的是s指针集中的东西，也需要加入到t的指针集里面

Propagate(n,delta) 这里面delta表示变量n的增量

如果delta不为空 那么就union 加入到ptn之中

如果在PFG中 n还有后继 n->s这类

那么就向WL中新增一个entry<s,delta> 表示delta也要加入到n后续那些人的指针集里面

大循环

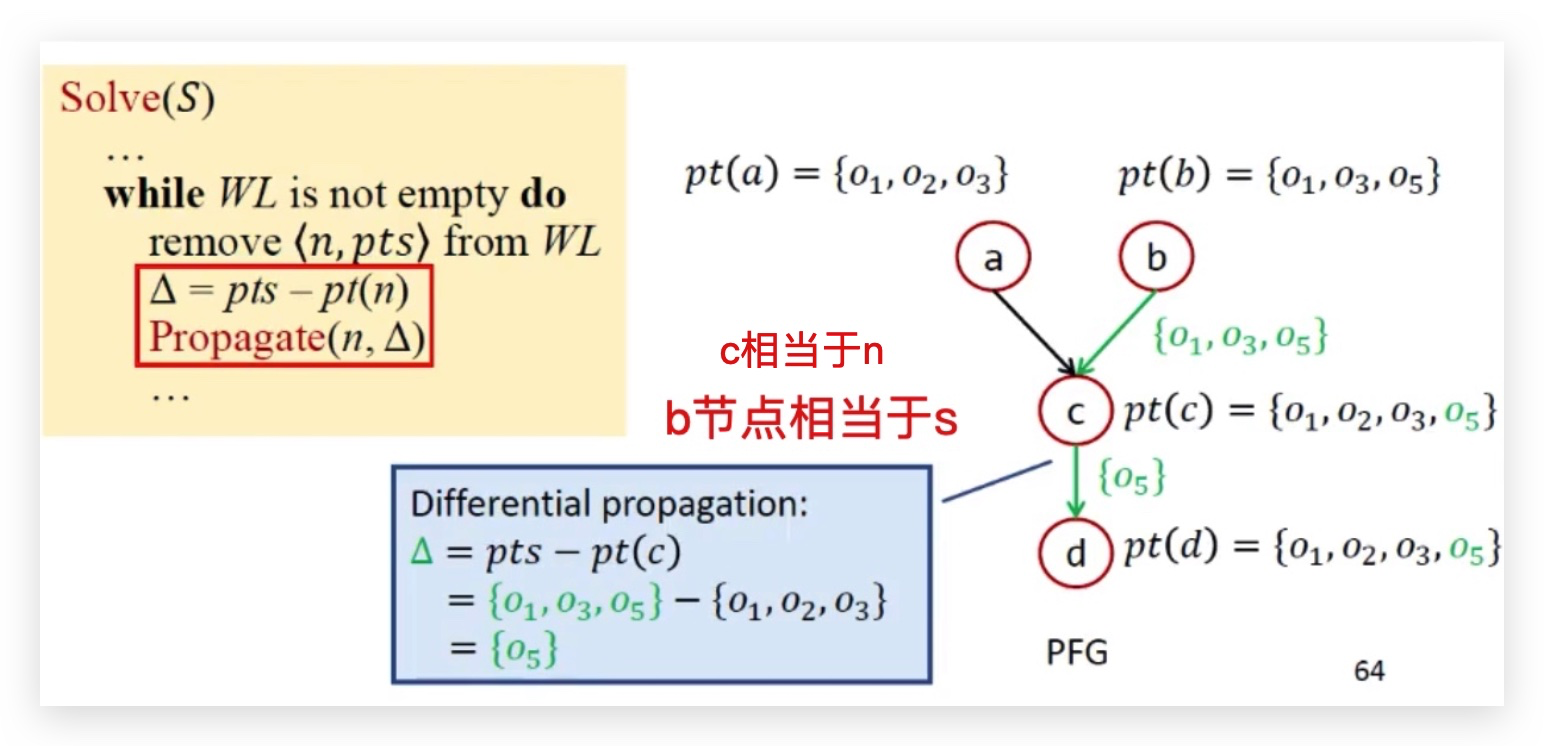
取出WL中的一个entry <n,pts> 计算delta 紧接着Propagate(n,delta)

接下来如果n是一个变量，如果存在x.f的store和load的话，addEdge分别加边

delta是怎么来的？

pts中可能已经有一些对象是ptn中已经存在的了，所以需要去重。

delta中真正存在的是新增的，需要后续一串连锁反应。

强化一下AddEdge算法：

AddEdge(s，t)的意思就是如果PFG里面没有，那么就新增一条s->t的边，

接下来不要忘了指向信息的传播，如果s的指针集里面还有东西，那么也要把s指针集里面的东西让t也能指到。也就是新增<t,pt(s)>到WorkList集合里面。

s = t ;
指向：----->
流向：<-----

对于上面这个语句：

s是指针，s指向了t，那么t属于pt(s)，pt(s)={t};

也可以理解为pt(t)指针集里面的东西向左流给了pt(s)，这里如果pt(t)里有东西，那么也要向左流给s，也就是pt(s)={pt(t)};

Oi.f可能会被别的变量指向

强化理解一下Propagate算法：参数是n、pts，这里的pts其实就是delta增量。

如果pts不是空集，那么就是把增量加入到ptn。

接下来还要把新的指针集都改了，继续传播下去。连锁反应。

取出所有的n指向的边，也就是n的后继s，将<s,pts>加入到WL中，这里其实就是将指向信息传递给同名指针。

例子

流不敏感指针分析

	WL	正处理	PFG	指针集	处理语句	算法语句
1	[<b, {o1}>, <c, {o3}>]				1，3	处理New
2	[<b, {o1}>, <c, {o3}>]		a <- b；d <- c；		2，4	处理Assign
3	[<c, {o3}>]	<b, {o1}>	a <- b；d <- c；	pt(b)={o1}		while开头
4	[<c, {o3}>], [<a, {o1}>]		a <- b；d <- c；			Propagate()传递，没有b.f语句
5	[<a, {o1}>]	<c, {o3}>	a <- b；d <- c；	pt(c)={o3}		while开头
6	[<a, {o1}>, <d, {o3}>]		a <- b；d <- c；			Propagate()传递，有c.f语句
7	[<a, {o1}>, <d, {o3}>]		a <- b；d <- c；o3.f <- a；o3.f <- d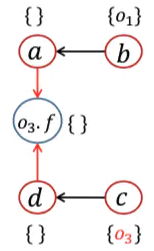；		4，6	处理Store/Load，添加边
8	[<d, {o3}>]	<a, {o1}>		pt(a)={o1}；		while开头
9	[<d, {o3}>,<o3.f, {o1}>]		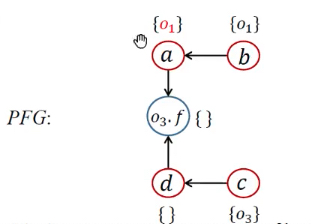			Propagate()传递
10	[<o3.f, {o1}>]	<d, {o3}>		pt(d)={o3}		while开头
11	[<o3.f, {o1}>, <o3.f, {o3}>]		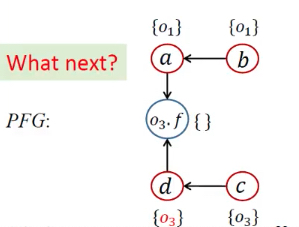			Propagate()传递，有d.f语句
12	[<o3.f, {o1}>, <o3.f, {o3}>]		a<-b；d<-c；o3.f<-a；o3.f<-d；e<-o3.f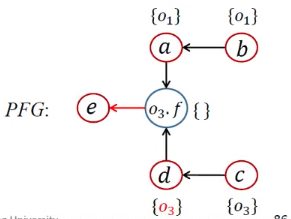；		7	处理Load，添加边
13	[<o3.f, {o3}>]	<o3.f, {o1}>		pt(o3.f)={o1}；		while开头
14	[<o3.f, {o3}>, <e, {o1}>]		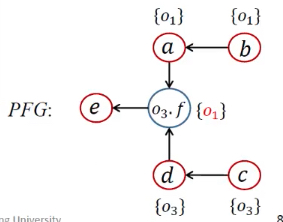			Propagate()传递
15	[<e, {o1}>]	<o3.f, {o3}>		pt(o3.f)={o1, o3}		while开头
16	[<e, {o1}>, <e, {o3}>]		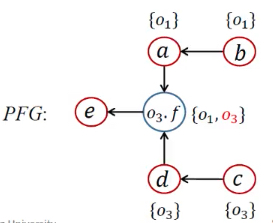			Propagate()传递
17		<e, {o1}>；<e, {o3}>		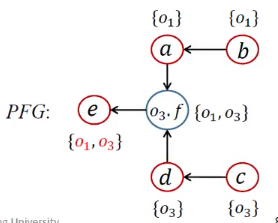pt(e)={o1, o3}		while开头

---

1. 第一看new 语句，分别有1、3两处、直接添加到WL中

   WL：<b,o1>,<c,o3>

2. 第二看assign语句，分别有2、4两处。需要进入到addEdge函数语句

   由于PFG此时还是空的，向PFG增加两条边

   目前pta、ptb都是空的，所以不添加WL

   WL：<b,o1>,<c,o3>

   PFG: a<-b , d<-c

3. 进入大循环，取出来<b,o1>，delta就是o1,进入Propagate函数

   更新ptb为o1，b此时有后继a，需要增加<a,o1>到WL

   由于没有b.f的操作，所以本次循环直接结束

   WL：<c,o3>,<a,o1>

   PFG:

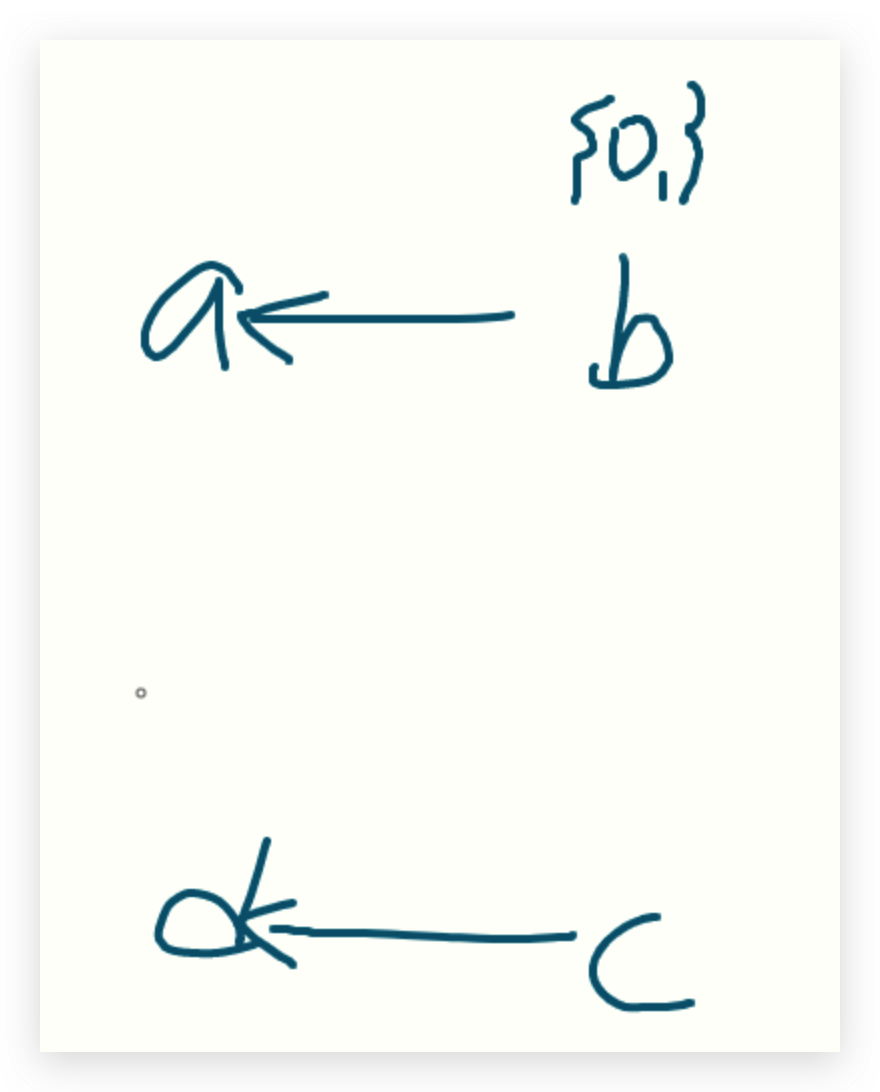
4. 取出<c,o3>，delta就是o3，进入Propagate函数

   更新ptd为o3，c此时有后继d，需要增加<d,o3>到WL

   WL: <a,o1>,<d,o3>

   PFG:

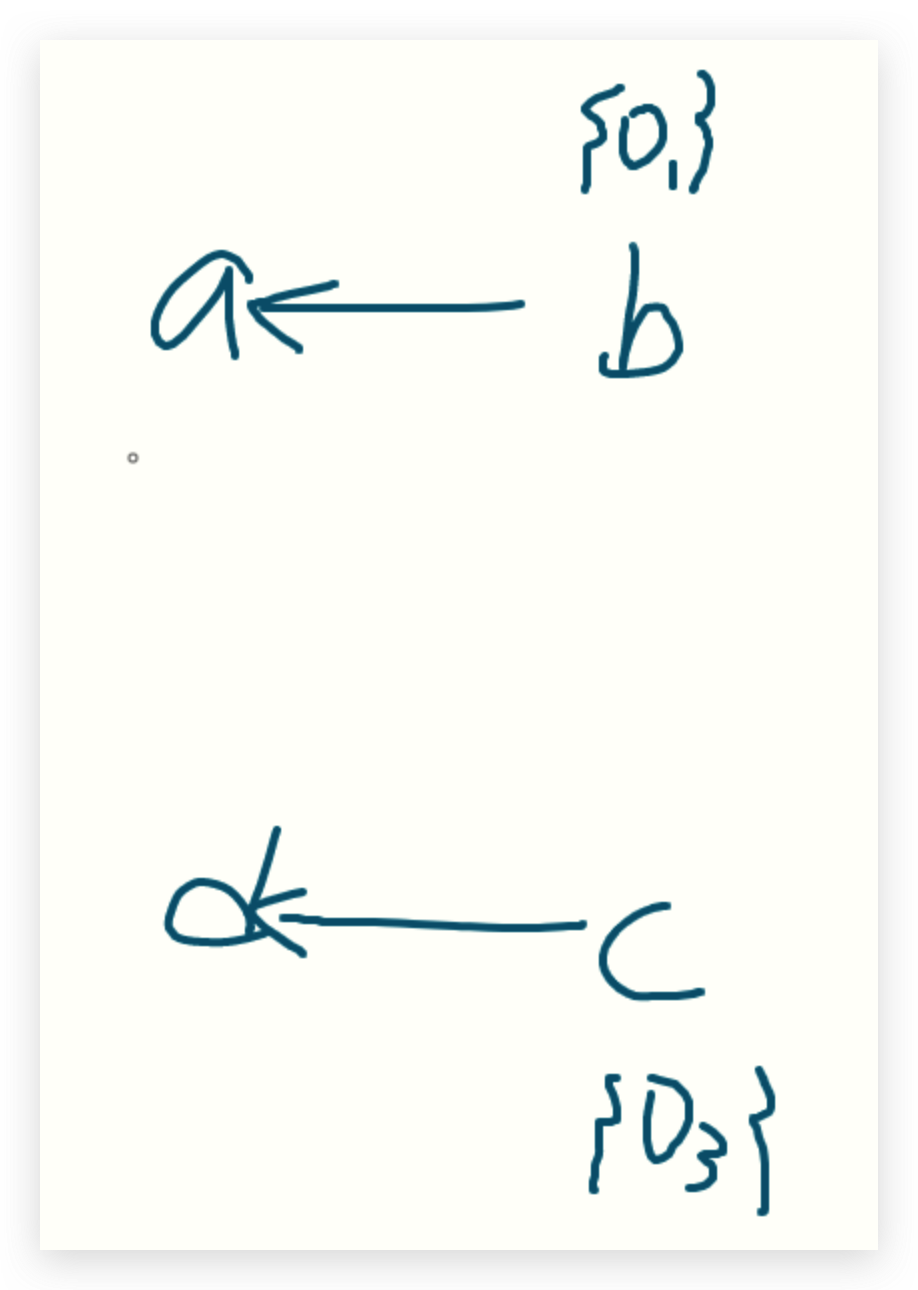
   接下来，当前分析的对象是c，由于存在c的load和store语句，需要进行field的加边

   4处：c.f=a -> addEdge(a,o3,f)

   addEdge(a,o3,f)：首先由于不存在a->o3.f的边，直接加上a->o3.f这条边

   由于pta目前为空，跳过

   WL：<a,o1>,<d,o3>

   同理，6处：c.f=d -> addEdge(d,c.f)

   addEdge(d,c.f) : 首先还是不存在d->c,f这样的一条 直接加上d->c,f

   由于ptd目前为空 跳过

   WL：<a,o1>,<d,o3>

   目前PFG：

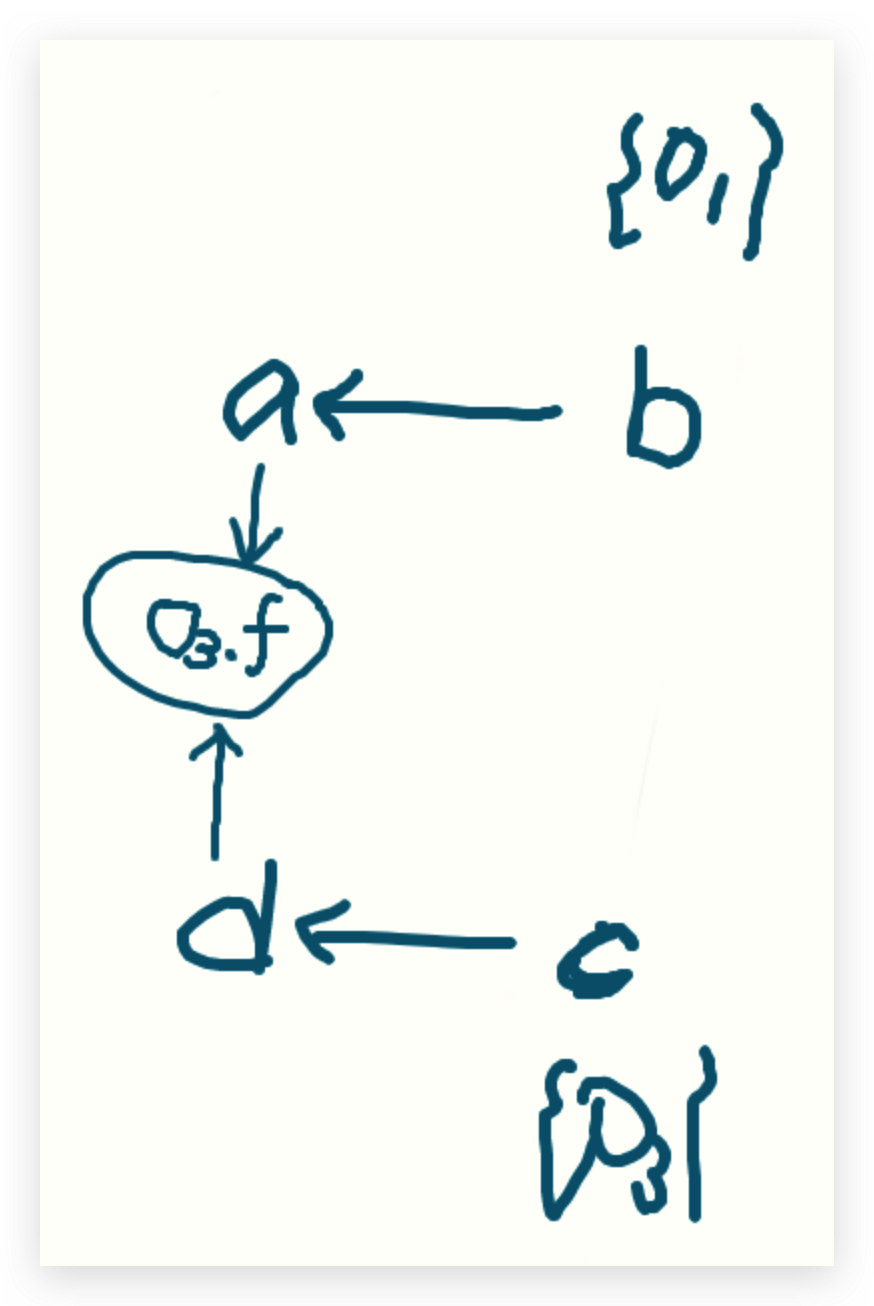
5. 接下来继续处理WL 该到<a,o1>,<d,o3>了

   这两个是一个类型 所以我就直接一起写了

   <a,o1>：delta就是o1,pta加上o1，

   这时候a的后继就是o3.f，需要向WL中增加<o3.f,o1>

   由于没有a的field操作，所以跳

同理<d,o3>：delta就是o3,ptd需要加上o3

此时d的后继也是o3.f所以也需要向WL增加<o3.f,o3>

此时由于7处出现了e=d.f 是一个load语句，执行addEdge(o3.f,e)

需要加一条边 也就是o3.f->e

WL：<o3.f,o1>，<o3.f,o3>

PFG：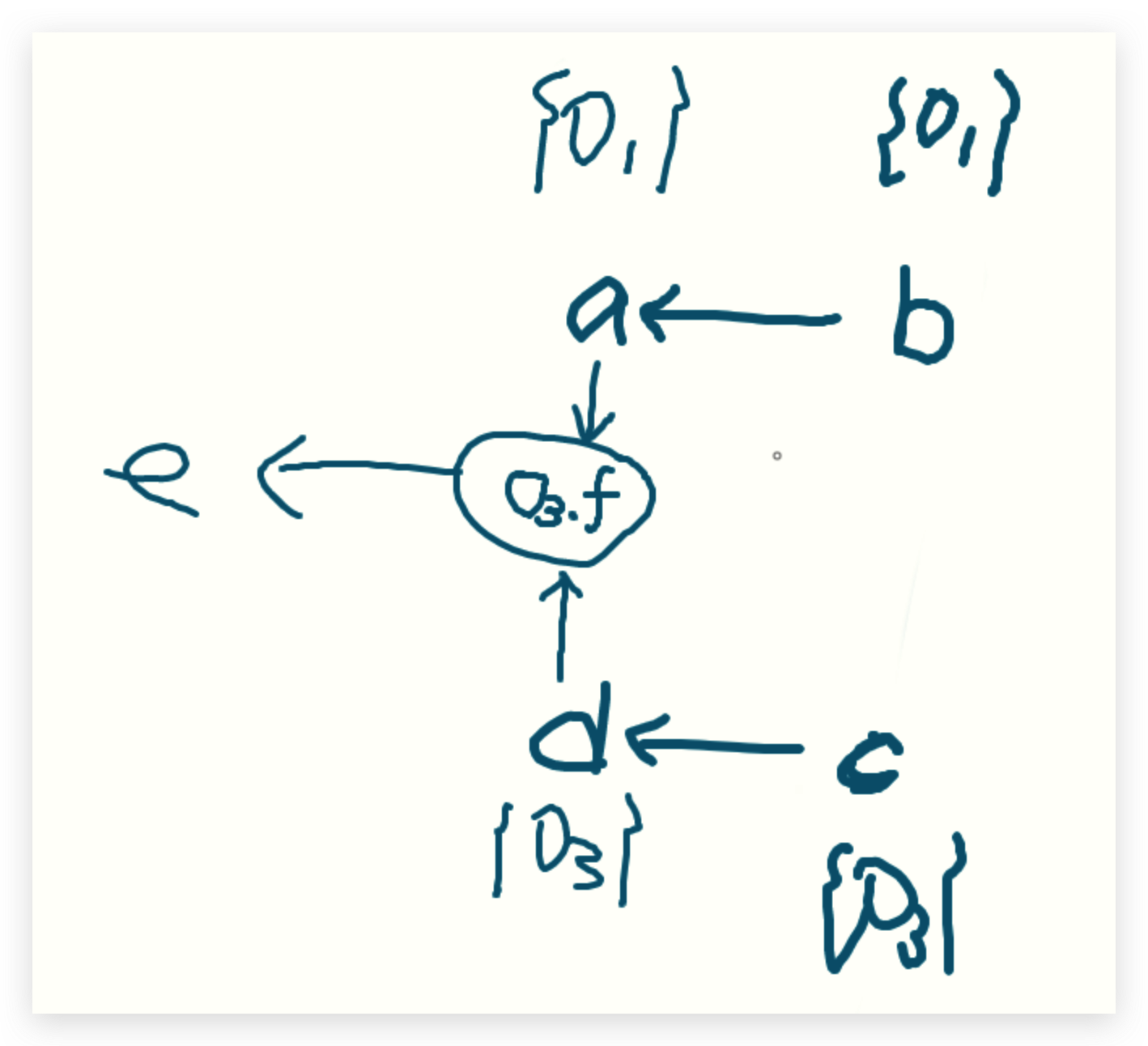

6. 接下来解析<o3.f,o1>，delta是o1，所以把o1加入到o3.f的指针集里面

   由于o3.f有后继e,因此也是需要把<e,o1>加入到指针集

7. 接下来解析<o3.f,o3>，delta是o3，所以把o3加入到o3.f的指针集里面

   由于o3.f有后继e,因此也是需要把<e,o3>加入到指针集

   WL：<e,o1><e,o3>

   PFG:

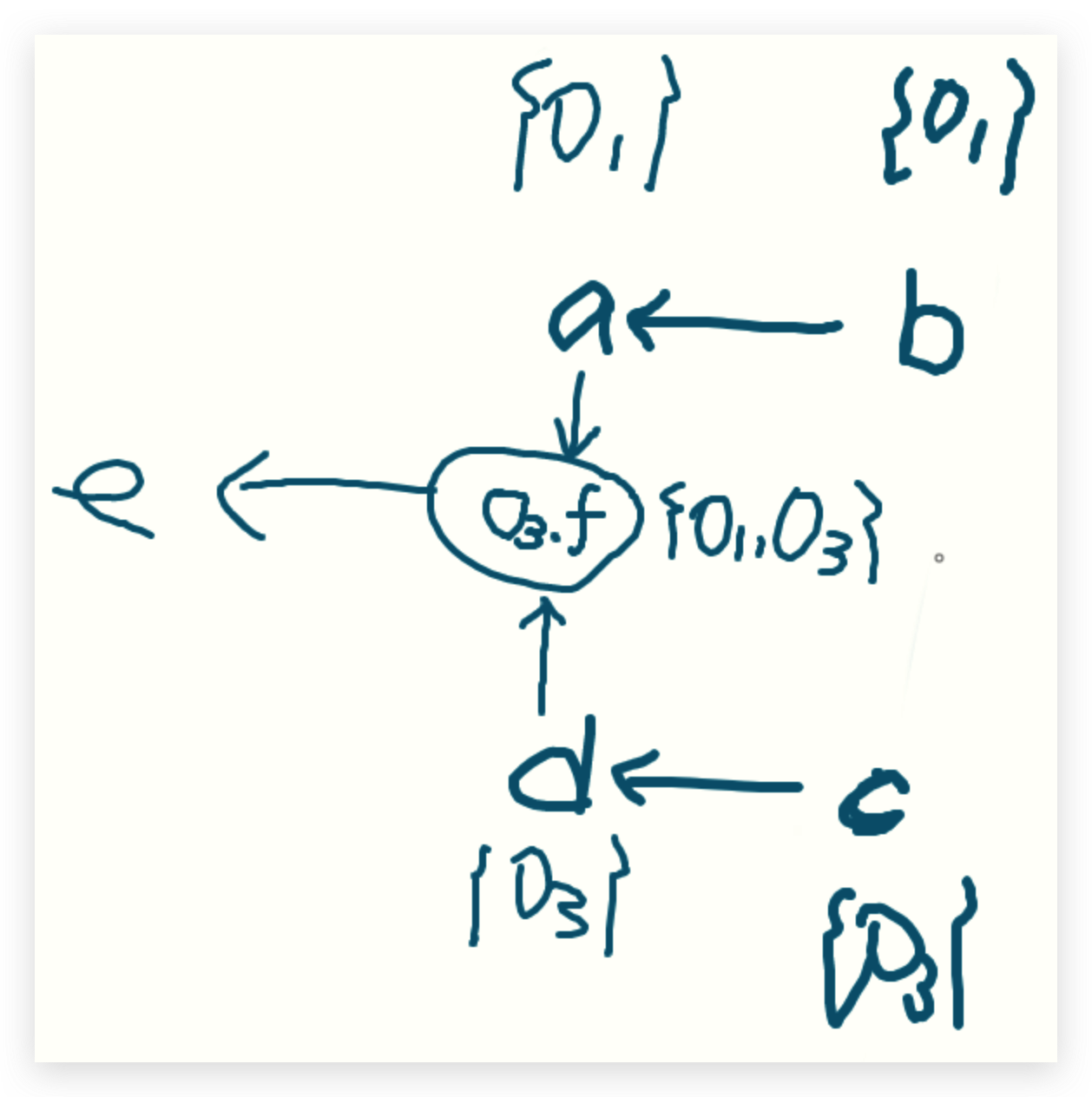
8. 最后处理<e,o1><e,o3>，分别就是向e的指针集里面增加两项o1,o3

9. 最终PFG：

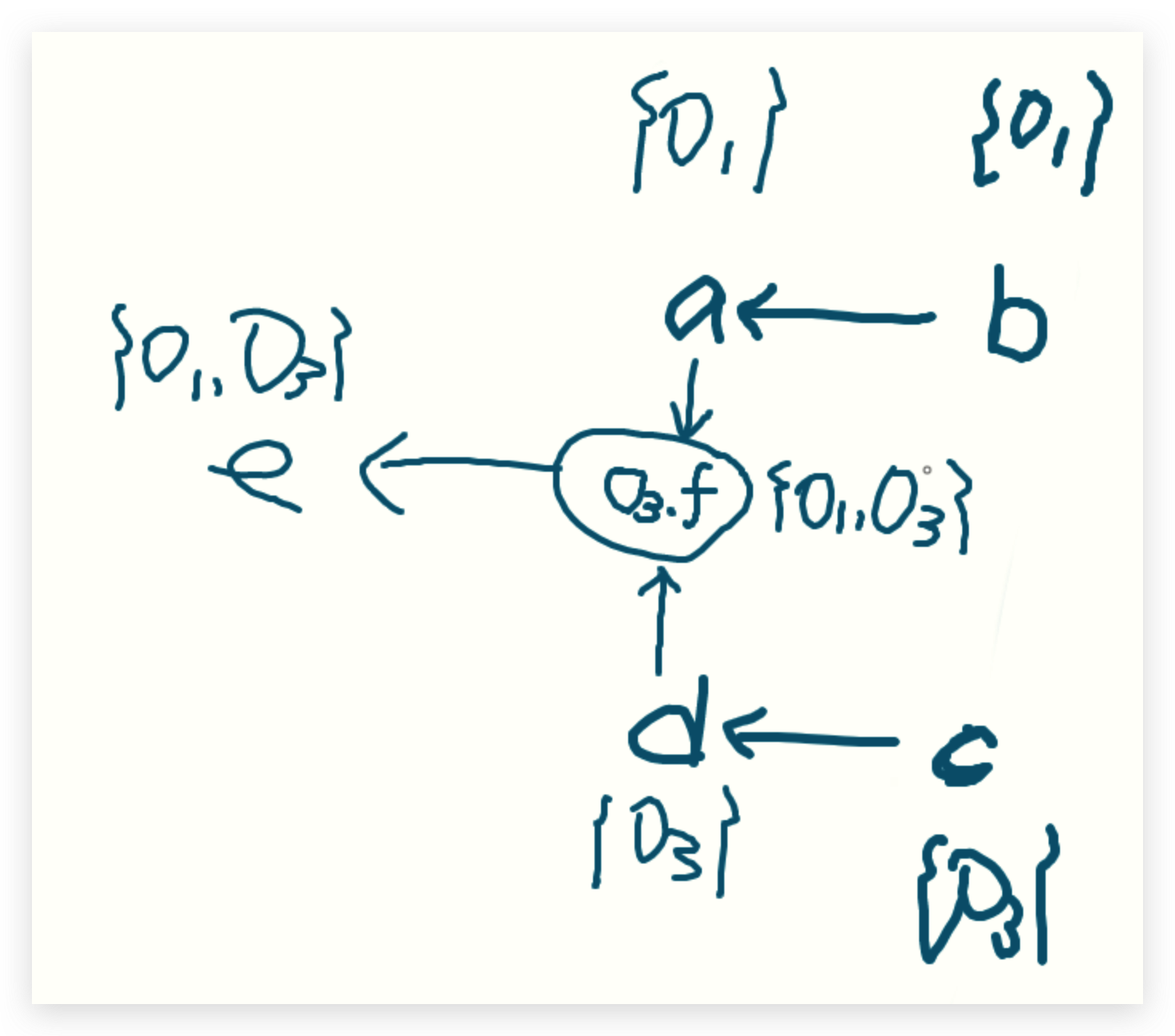
课后总结：

有人提问：流敏感指针分析有什么区别？

TT答：流敏感指针分析是在程序的特定运行位置维护一个指针集，对于Java来说开销极大并且benifit不明显，所以在Java业界主要还是流不敏感的指针分析。如果提升精度，主要选择上下文敏感的指针分析。

上述算法和WALA的实现比较像。

有人提问：PFG用途？

TT答：如果你想要追踪对象如何在指针之间流动的话，PFG可以帮你做到。

10

指针分析处理函数调用

构造调用图技术对比：

• CHA：基于声明类型，不精确，引入错误的调用边和指针关系。
• 指针分析：基于pt(a)，即a指向的类型，更精确，构造更准的CG并对指针分析有正反馈（所以过程间指针分析和CG构造同时进行，很复杂）。aka. on-the-fly call-graph construction

void foo(A a) {   
  // pt(a) = ???
  ...
    b = a.bar();    
  // pt(b) = ???  把a的指向分析清楚了，就能确定a.bar()到底调用哪个对象的bar()函数，那么b的指向也明确了。
    ... 
}

Call调用语句规则

call语句规则：主要分为4步。

1. 找目标函数m：Dispatch(oi, k)——找出pt(x)，也即oi类型对象中的k函数。
2. receiver object：把x指向的对象（pt(x)）传到m函数的this变量，即mthis
3. 传参数：pt(aj), 1<=j<=n 传给m函数，即p(mpj), 1<=j<=n。建立PFG边，a1->mp1，…，an->mpn。
4. 传返回值：pt(mret)传给pt(r)。建立PFG边，r <- mret。

问题：为什么PFG中不添加x->mthis边？

答：因为this只和自己这个对象相关，而可能有pt(x)={new A, new B, new C}

指定对象的x只流向对应的对象，是无法跨对象传递的。

连上这条this边，就会有很多错误的边。

参数没法决定receiver object是哪个 所以随便连 没关系的

过程间PTA算法

问题：由于指针分析和CG调用图的构造互相依赖，所以每次迭代只分析可达的函数和语句。然后不断发现和分析新的可达函数。

方法：“一起做”。从main入口开始做，开始建边，分析可达性方法，不断挖掘。

对于某一段程序，仅仅分析他的可达性方法，reacheable世界，其余方法对于他来说都是“不存在”的

可达示例：

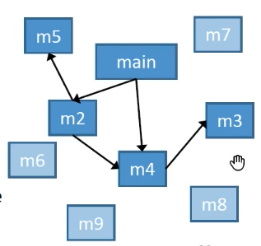
算法：

上下文不敏感 每个方法只统计一次

符号：

• m_entry：入口main函数
• Sm：函数m中的语句
• S：可达语句的集合（就是RM中的语句）
• RM：可达函数的集合
• CG：调用图的边

理解：

1. AddReachable就是拓展世界的函数，只有两处会调用：

   1. 程序入口点；
   2. 新的调用边被发现；

   在新方法加入之后，先只看new和assign赋值语句，因为load和store是随着指针集的变化而变化，先研究也没有意义。

2. ProcessCall里面，x表示的是一个变量，是receiver object，oi表示的是流向x的某个新来的对象。

   首先遍历与x有关的调用语句，先调用dispatch，取出真正的目标方法m

   接下来将<this,oi>加入到worklist中，也就是将receiver object传递给this变量

   l就是call site，m就是解出来的目标方法

   如果l-m这条边在CG中没有的话，添加一条边

   AddReachable拓展m方法

   传递形参

   传递返回值

3. 问题：为什么ProcessCall(x, oi)中，要判断L->m这条边是否已经加入到CG？因为x可能指向多个对象，就会多次处理L这个调用指令，可能x中别的对象oj早就已经将这条边加入进去了。

4. AddReachable

   拓宽可达性方法的世界

   如果m不在可达方法合集中，m加入到RM，并且m方法中的语句(Sm)加入到所有可达方法(S)

   对于Sm中出现的new语句：和PTA一样加入到WL中

   对于Sm中出现的assign语句：x=y AddEdge(y,x)

ProcessCall(x,oi)

x是WL中<n,pts>中n所代表的变量，oi属于n指针集的变化

对于S中调用语句l: r = x.k(a1,...,an)

1 m = Dispatch(oi，k) 去解目标方法，也就是当前receiverObject是oi情况下，真正的方法

2 传this <m.this,oi>加入到WorkList中

如果l->m这条边不存在于CG中：

加上这条边

AddReachable(m) 将我们的m方法加入到可达方法的集合内

3 AddEdge(ai,pi) 传递参数 实参->形参

4 AddEdge(mret,r) 传递返回值

例子

	WL	正处理	PFG	指针集	RM	CG	语句	算法语句
1	[]		{}		{}	{}		初始化
2	[]				{A.main()}		1，2	AddReachable(mentry)
3	[<a,{o3}>, <b,{o4}>]						3，4
4	[<b,{o4}>]	<a,{o3}>		pt(a)={o3}；				while开头
5	[]	<b,{o4}>		pt(b)={o4}				while开头
6	[]						5	ProcessCall(b, o4)
7	[<B.foo/this, {o4}>]					{5->B.foo(A)}		m=Dispatch(o4, foo())=B.foo()；添加到调用图
8	[<B.foo/this, {o4}>, <r, o11>]				{A.main(), B.foo()}			AddReachable(B.foo())；添加到可达函数
9	[<B.foo/this, {o4}>, <r, o11>, <y, {o3}>]		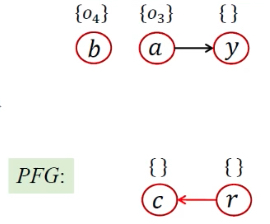					AddEdge()；添加参数边、返回值边
10	[<r, o11>, <y, {o3}>]	<B.foo/this, {o4}>		pt(B.foo/this)={o4}；				while开头，B.foo/this没有调用任何函数
11	[<y, {o3}>, <c, {o11}>]	<r, o11>		pt(r)={o11}；				while开头
12		<y, {o3}>, <c, {o11}>		pt(y)={o3}；pt(c)={o11}				while开头

如果是CHA的话，CG={5->B.foo(A), 5->A.foo(A)}，错误识别为调用边。

1. 首先m[entry]当然是main方法了，RM中加入main，S中加入main方法的语句

   main方法内出现了3、4两行的new，向WL中添加<a,o3><b,o4>

2. 进入到大循环，首先取出<a,o3>，delta为o3，propagate(a,o3)做了很多事，首先将a的指针集加入o3，加下来尝试寻找a的后继，但是目前还是没有，于是返回。回到外边，尝试寻到a的store/load相关的操作，未果，结束。

3. 接下来轮到<b,o4>，delta为o4，propagate(b,o4)做了很多事，首先将b的指针集加入o4，加下来尝试寻找b的后继，但是目前还是没有，于是返回。回到外边，尝试寻到b的store/load相关的操作，未果，进入到ProcessCall。

4. ProcessCall(b,o4) 首先处理Dispatch的结果m就是B.foo(A)，接下来传this，WL里面传进去：<B.foo/this,o4> ，然后由于CG是空的，于是建立一条5->B.foo(A)的calledge。

5. 这时候也就是说，我们的可达性方法里面出现了一个新的方法B.foo，因此需要用AddReachable(B.foo(A))方法。

6. AddReachable(B.foo(A))做了哪些事呢？首先，加RM集合，加Sm语句不多说了，接下来就是new 处理 assign两种语句。仅仅发现10行有一个new 将<r,o11>加入到WL中

7. 接下来传递参数AddEdge(a,y)，进入AddEdge方法，建立PFG的边a->y， 由于a的指针集目前还有一个o3,那么就需要向WL中加入<y,o3>

8. 最后传递返回值，AddEdge(r->c)，进而建立一条PFG的边r->c

9. 进入下一次循环，取出<B.foo/this,o4>，delta就是o4，在PFG中，B.foo/this的指针集的内容就是o4，其他什么都不做。

10. 下一个<r,o11>, 首先delta就是o11，r的指针集的内容添加一个o11，r的后继有c，于是WL中添加<c,o11>

11. 目前WL中只有<y,o3>和<c,o11>。对于这两个，都是将y和c的指针集新增delta，其余什么都没做。

结果：

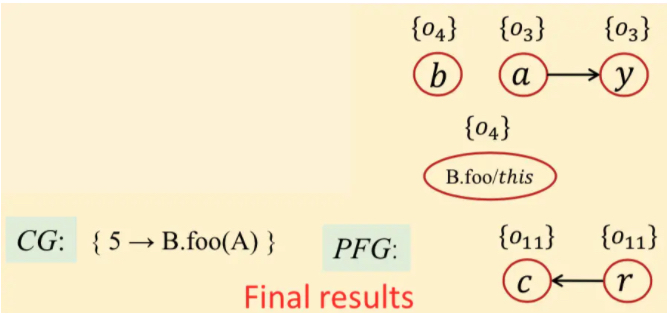
问题：没有入口函数的？如对库函数处理，生成调用库函数的程序。

理解4条rule： dispatch解目标方法，传this，传参数，传返回值

11

上下文不敏感分析

说明：上下文敏感分析是对指针分析的准确性提升最有效的技术。

问题：上下文不敏感时，分析常量传播这个问题，由于没有明确调用id()的上下文，会把不同的调用混在一起，对id函数内的变量n只有一种表示（没有对局部变量进行区分），导致n指向的对象集合增大，将i识别为非常量NAC。实际上，x.get()的值只来自于One()对象，i应该是常量1。

解决：根据调用的上下文（主要有3种：如根据调用点所在的行数——call-site sensitivity）来区分局部变量。

上下文敏感分析 C.S.

概念：

• call-site sensitivity (call-string)：根据调用点位置的不同来区分上下文，3：id(n1) / 4：id(n2)。
• Cloning-Based Context Sensitivity：每种上下文对应一个节点，标记调用者的行数。克隆多少数据，后面会讨论。
• Context-Sensitive Heap：面向对象程序（如Java）会频繁修改堆对象，称为heap-insensitive。所以不仅要给变量加上下文，也要给堆抽象加上下文，称为heap context（本课程是基于allocate-site来进行堆抽象的）。

Context Insensitivity 上下文不敏感的原因：

• 在动态执行的过程中，一个方法可能在不同的上下文条件下被调用多次。
• 在不同的上下文过程中，方法的参数返回值也会指向不同的对象。
• 在上下文不敏感的分析中，不同上下文调用的参数会被混合，然后会将错误结果传播继续往下传播，造成不准确

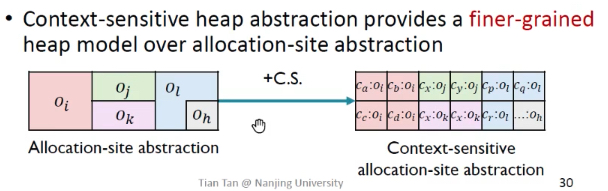
会得到粒度更细的堆抽象

堆抽象上下文示例：

堆抽象+上下文不敏感：如果不区分8 ：X x = new X();调用的堆抽象的上下文，导致只有1个o8.f，把两个上下文调用产生的o8.f指向集合都合并了，得出了o8.f的错误指向的结果。

堆抽象+上下文敏感：用不同的调用者来区分堆抽象，如3:o8、4:o8是不同上下文创建的堆抽象。所以说，既要根据上下文的不同来区分局部变量，也要区分堆抽象，例如：3:p是给变量加上下文，3:o8是给堆抽象加上下文。

规则：变量上下文标号和堆上下文标号都是缺一不可的。谁敏感谁加行号区分，行号其实就是上下文环境。

上下文敏感指针分析：规则

指针两种：变量 & field

标记：根据调用者的行数来区分不同上下文，只要区分了函数、变量、堆对象，就能够区分实例域、上下文敏感的指针（变量+对象域）。C—上下文（暂时用调用点的行数表示），O—对象，F—对象中的域。

方法、变量、对象都需要上下文前缀

field不存在上下文，但是实例对象的object的Instance fields是有上下文前缀的

指针(上下文敏感指针的)指向的对象是有上下文前缀的

基本规则：跟之前区别不大，只是增加了个上下文标记，有细微区别。

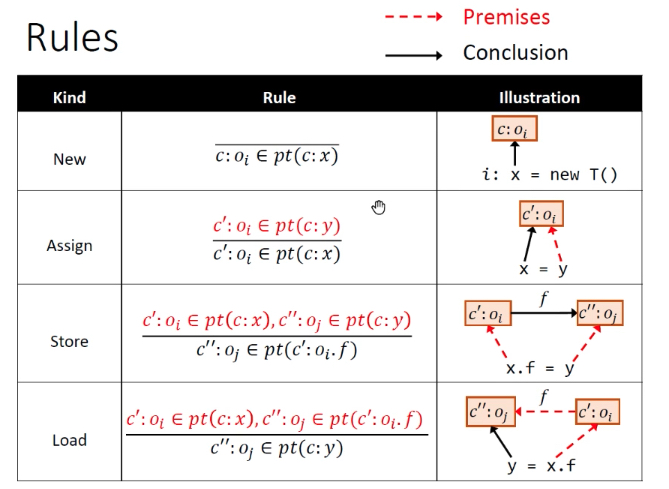
很经典的一张图，值得细细品味。

解读：

1. 首先l: r = x.k(a1,...,an)意思是在c上下文中，x所指向oi的对象，oi它的上下文为c’
2. 第二步，解析目标方法，依然是dispatch
3. 多了一步，select 选择方法的上下文，对于目标函数m选择上下文，根据调用点的信息，获得不同上下文条件下的目标方法ct
4. 传this：传的是ct上下文条件下m方法的this变量
5. 传参数：也是在特定上下文方法下的参数，会区分开数据流
6. 传返回值：从哪来，回哪里去。（不敏感就是到处瞎走，导致数据流混乱，敏感就是自己知道该回哪去）

Context Sensitive Pointer Analysis：Algorithms

区别：和过程间指针分析相比，仍然分为两个过程，分别是构造PFG和根据PFG传递指向信息。主要区别是添加了上下文。

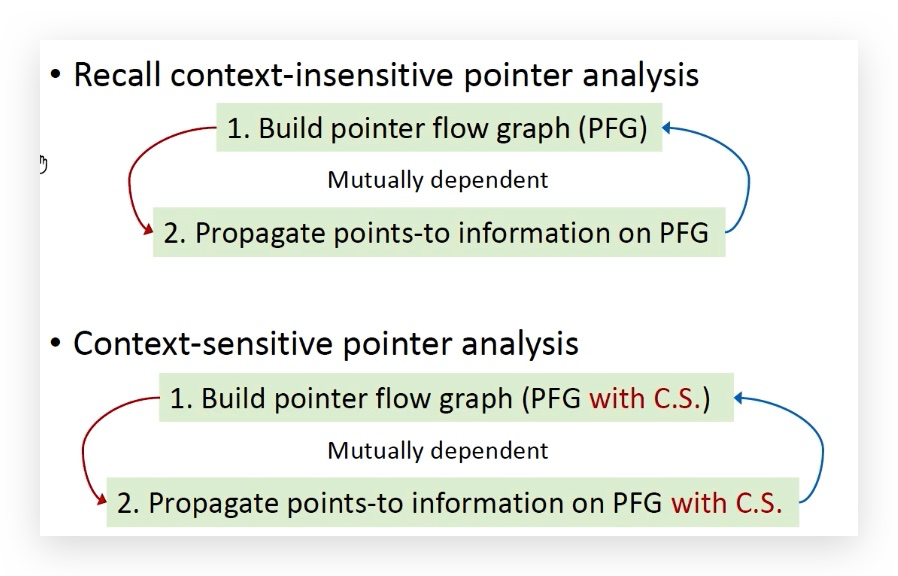
PFG构造：边添加规则和之前一样，Assign、Store、Load、Call，Call需要加参数传递、返回值传递的边。

节点为上下文敏感的指针，每个节点都带有上下文的信息；

边：节点之间的关系，指针集的流向关系。

其实就是每个关键的上下文都需要记录下来

符号：

• S：可达语句的集合（就是RM中的语句）
• Sm：函数m中的语句
• RM：可达函数的集合，带有上下文信息
• CG：调用图的边，带有上下文信息

Context Sensitivity Variants 上下文Select函数选取规则

上下文的选取主要采用3类：

• Call-Site Sensitivity
• Object Sensitivity
• Type Sensitivity
• …

说明：Select(c,l,c’:o_i,m)，c—调用者上下文，l—调用者语句，c’:o_i—接收对象（含堆的上下文信息）,m目标方法。

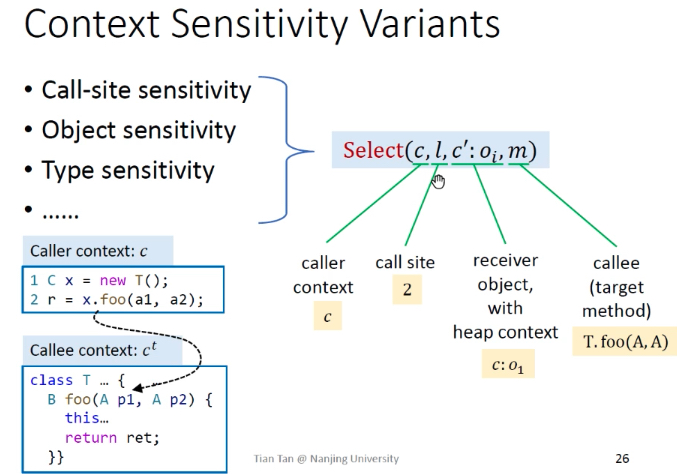
Call-site Sensitivity

对于一个正常函数的上下文，他会有很多callsite，这些callsite组合成一个chain，会有很多前驱的调用方法轨迹。

原理：又称为k-call-site sensitivity / k-CFA(Control-Flow Analysis)，不断添加调用行号。

Select(c,l,c’:oi,m) = (l’,…,l’’, l)

维护一个抽象调用栈。

问题：如果函数调用自身，导致无限递归，如何限制上下文长度？

解决：k-limiting Context Abstraction。对上下文加以限制，只取最后k个上下文，通常取k<=3。

例如，函数方法的上下文通常取2，堆上下文通常取1。

示例：采用1-Call-Site，省略heap上下文。

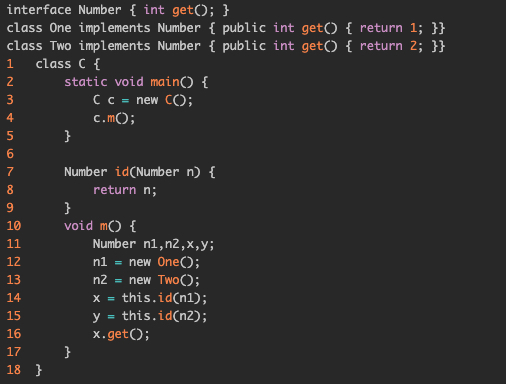
步骤：

初始化全部为空，接下来AddrReachable处理入口方法，上下文为空[]。首先入口方法为main方法，进到AddReachable之后，RM可达方法集合为{[]:C.main()}，WL中添加[<[]:c,{o3}>]注意是带有上下文的。接下来处理WL中的项，先做差集，o3加到带有上下文的指针集。这里没有load和store，走到processcall。进到processcall之后，select结果ct是4，代表是第四行进行了调用。接下来传递receiverobject，也就是[<[4]:C.mthis,{o3}>]放到WL中，表示将o3传递给4环境下的C类的this对象，接下来构建CG，也就是{[]:4->[4]:C.m()}表示在上下文为起始方法时，在第四行调用了C类的m方法，并且调用时候的上下文是4也就是在第四行调用的。接下来AddReachable，这时候RM可达方法集合为{[]:C.main(),[4].C.m()}，处理new语句，WL现状：[<[4]:C.mthis,{o3}>,<[4]:n1,{o12}>,<[4]:n2,{o13}>]表示在上下文为4的背景下，new出来了两个对象，分别在第12行和第13行创建。然后传参传返回值都是空，所以结束。

接下来处理WL中的下一个，应该是<[4]:C.mthis,{o3}>，首先propagate，算差集，this之前指针集还是空，那么o3就放到[4]:C.mthis的指针集里面。往下走，没有load和store，但是有两个方法调用，那么进入processcall，dispatch求得目标函数为m=C.id(Number)，上下文ct为[14]，往下走，先处理14行的上下文：构建CG调用边，CG目前现状：{[]:4->[4]:C.m(),[4]:14->[14]:C.id(Number)}，AddReachable将RM更新为{[]:C.main(),[4].C.m(),[14]:C.id(Number)}表示新添加的方法可达，接下来传参，[4]:n1->[14]:n表示n1参数作为实参传递给14行的形参；传返回值也类似：[14]:n->[4]:x表示14行的n作为返回值，传递给了4上下文下的x。接下来处理15行的上下文，m还是m=C.id(Number)，上下文ct为[15]，CG为：{[]:4->[4]:C.m(),[4]:14->[14]:C.id(Number),[4]:15->[15]:C.id(Number)}，RM为{[]:C.main(),[4].C.m(),[14]:C.id(Number),[15]:C.id(Number)} ，接下来传参，[4]:n2->[15]:n ，传返回值[15]:n->[4]:y 这也就是通过上下文将数据流分开。

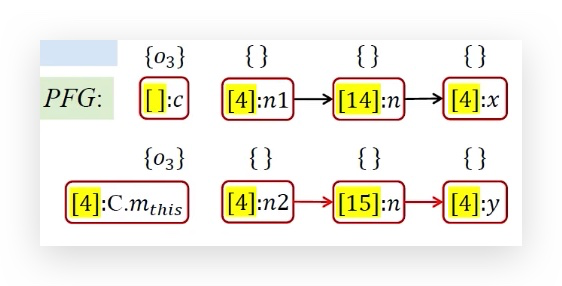
接下来继续处理WL里面剩余的参数，该轮到<[4]:n1,{o12}>和<[4]:n2,{o13}>了 这里同理快进，其实就是把o12和o13接到了PFG上面，开始传播

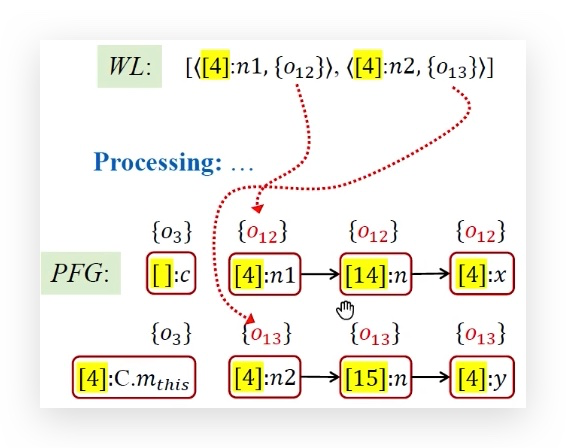
当o12传递给x之后，执行x.get()方法调用

最终结果：

<img src=”../images/%E3%80%90%E5%8D%97%E4%BA%AC%E5%A4%A7%E5%AD%A6-%E8%BD%AF%E4%BB%B6%E5%88%86%E6%9E%90%E3%80%91%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/image-20210413110839543.png” alt=”image-20210413110839543” style=”zoom:50%;” /

	WL	正处理	PFG	指针集	RM	CG	处理语句	算法语句
1					{[]:C.main()}		3	AddReachable(mentry)—加入RM
2	[<[]:c, {o3}>]						3	AddReachable(mentry)—处理New
3	[]	<[]:c, {o3}>		pt([]:c) ={o3}；				While开头，Propagate()—遍历WL更新指针
4	[⟨[4]:C.mthis, {o3}⟩]						4	ProcessCall()—this指针加入WL
5	[⟨[4]:C.mthis, {o3}⟩]					{[ ]:4 → [4]:C.m()}；		ProcessCall()——函数加入CG
6	[⟨[4]:C.mthis, {o3}⟩，⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]		没有参数/返回值		{[]:C.main(), [4]:C.m()}		12,13	ProcessCall():AddReachable(m)处理m函数中的New
7	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]	⟨[4]:C.mthis, {o3}⟩		pt([]:c) ={o3}；pt([4]:C.mthis)={o3}；				While开头，Propagate()—遍历WL更新指针
8	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]							ProcessCall():处理m中的this调用
9	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]						14	ProcessCall():Select(c,l,c’:oi)选择上下文ct=[14]
10	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]				{[]:C.main()， [4]:C.m()，[14]:C.id(Number)}	{[ ]:4 → [4]:C.m()；[4]:14 → [14]:C.id(Number)}；		ProcessCall():AddReachable([14]:C.id(Number))
11	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]		[4]:n1→[14]:n→[4]:x；					ProcessCall():AddEdge()参数边/返回值边
12	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]		[4]:n1→[14]:n→[4]:x；[4]:n2→[15]:n→[4]:y；		{[]:C.main()， [4]:C.m()，[14]:C.id(Number)，[15]:C.id(Number)}	{[ ]:4 → [4]:C.m()；[4]:14 → [14]:C.id(Number)，[4]:15 → [15]:C.id(Number)}；	15	ProcessCall()同理
13	[]	[⟨[4]:n1, {o12⟩，⟨[4]:n2, {o13⟩]		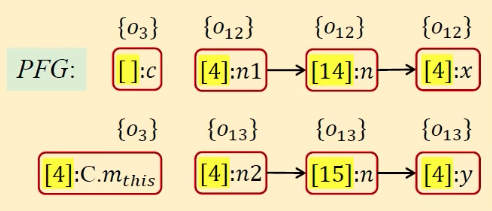				While开头—遍历WL更新指针
14	[]						16	While开头，ProcessCall()—处理x.get()

上下文不敏感vs上下文敏感（1-Call-Site）：

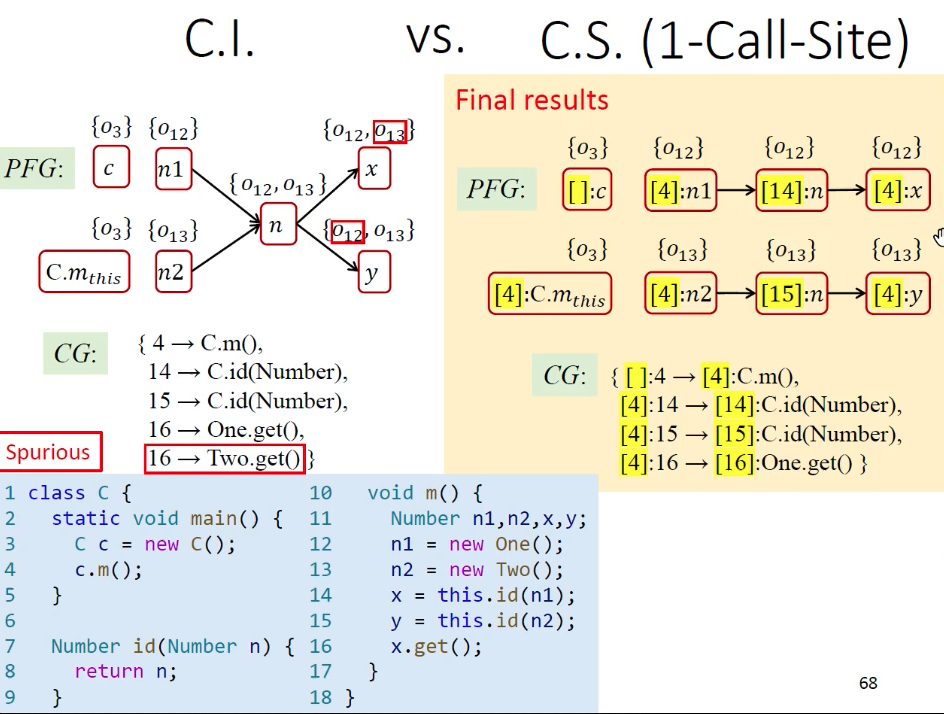
左边callsite不敏感会产生误报，认为16也会调用Two.get

Object Sensitivity

原理：针对面向对象语言，用receiver object来表示上下文。对比1层的调用点敏感和对象敏感，时间和准确性上对象敏感显然更优，这是由面向对象语言的特点所确定的。

Select(c,l,c’:oi,m) = [oj, … , ok, oi] （c’ = [oj, … , ok]）

示例：选取1-object，最终pt(x)=o3。

对比：对比1-Call-Site和1-object上下文，在这个示例中1-object明显更准确。原因是面向对象语言的特性，多态性产生很多继承链，一层一层调用子对象，其中最关键的是receiver object，receiver object决定了调用者的根源。本例有多层调用，若采用2-Call-Site就不会出错。

规律：this所指的变量一定是自己的上下文

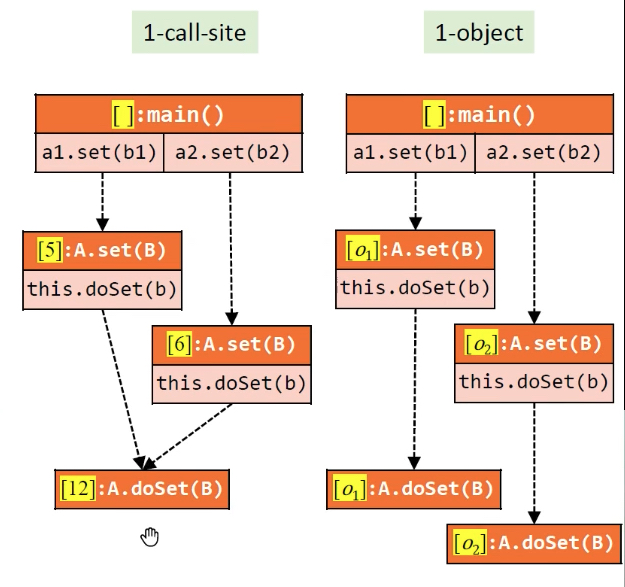
示例2：在本示例中，1-Call-Site明显更准确。因为同一个receiver object用不同参数多次调用了子函数，导致局部变量无法区分。

结论：所以理论上，object敏感与callsite敏感的准确度无法比较。但是对于面向对象语言，object敏感的准确度和效率要明显优于callsite敏感。

Type Sensitivity

原理：牺牲精度，提高速度。基于创建点所在类的类型，是基于对象敏感粗粒度的抽象，精度较低。

调用点所在的类型作为上下文；

总体对比

精度：object > type > call-site

效率：type > object > call-site

本课老师提出选择上下文的方法，对代码的特点有针对性的选择上下文方法。

Java分析不需要流敏感，开销太大了，效果不明显。

12 & 13

显示流和隐藏信道，使用污点分析来检测信息流漏洞。

信息流安全

访问控制：关注信息访问。但是程序获得信息之后去做了什么，访问控制监管不到。

信息流安全：关注信息传播。保证程序以安全的程序处理信息，防止泄露。

信息流：x->y表示x的值流向y。

信息等级：对不同变量进行分级，即安全等级，H-高密级，L-低密级。可以用格进行分类，给优先级排序。

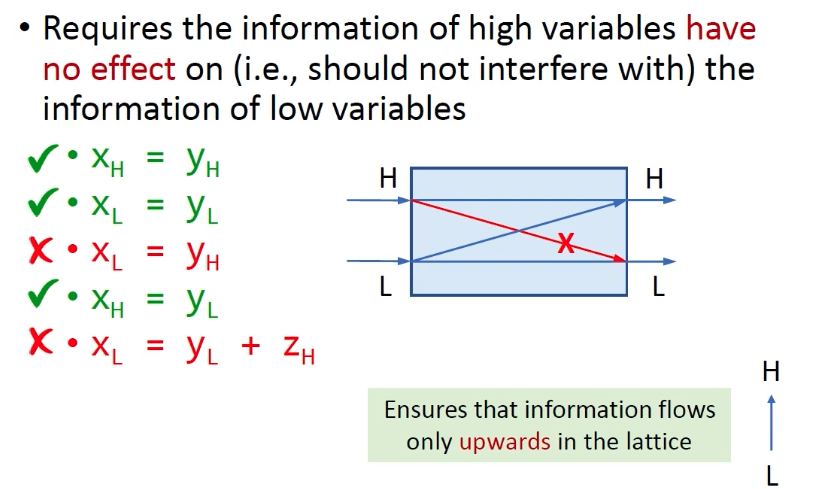
安全策略：非干涉策略，高密级变量H的信息不能影响（流向）低密级变量L。

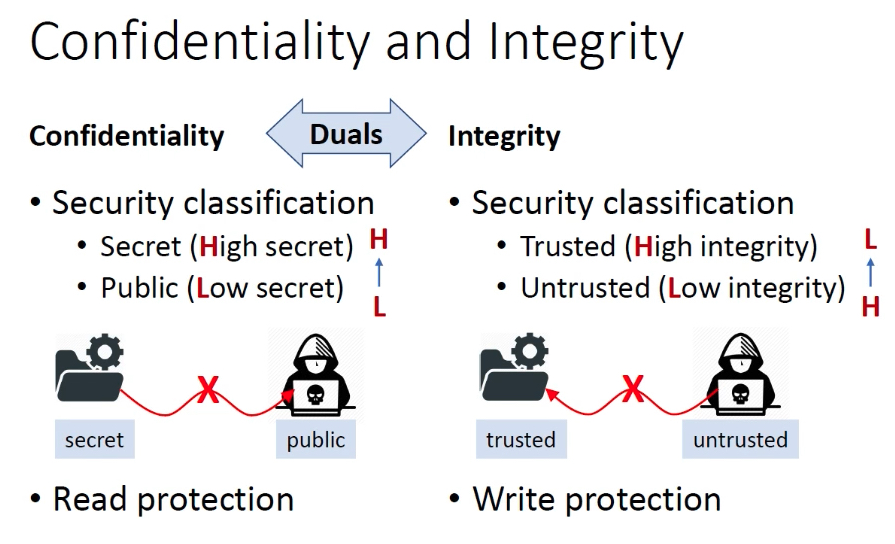
机密性和完整性

保密性—信息泄露，读保护；完整性—信息篡改，写保护。

完整性错误类型：命令注入、SQL注入、XSS攻击、… 。都属于注入错误。

完整性更宽泛的定义：准确性、完整性、一致性。准确性表示关键数据不被不可信数据破坏；完整性表示系统存储了所有的数据；一致性表示发送的数据和接收的数据是一致的。

显示流和隐藏信道-Explicit Flows and Covert Channels

显示流：直接用=数值传递。由于显示流能泄露更多信息，所以本课程关注显示流的信息泄露。

隐式信息流—侧信道：程序可能会以一些意想不到的方式泄露数据。

// Eg1 隐式流
if (secret_H < 0) 
  public_L = 1; 
else Public_L = 0;
// Eg2 终止信道
while(secret_H < 0) { ... };
// Eg3 时间信道
if (secret_H < 0)
  for (int i = 0; i< 1000000; ++i) { ... };
// Eg4 异常
if (secret_H < 0)
  throw new Exception("...");
// Eg5 如果访问数组越界，则可以推断secret可以为负数
int sa_H[] = getSecretArray();
sa_H[secret_H] = 0;

Covert Channels：信道指的是传递信息的机制，convert_channel指的是那些原本目的不是为了传递信息的信道。

污点分析

说明：使用最广的信息流分析技术，需将程序数据分为两类，把感兴趣的数据标记为污点数据。

核心：借助指针分析来传播污点数据，判断污点数据是否可以流到sink点中。

概念

Sources & Sink：

Sources是污点数据的源，一般是某些方法的返回值，如read()；

Sink是特定的程序点，某些敏感函数。

保密性：Source是秘密数据，Sink是泄露点，信息泄露漏洞。

完整性：Source是不可信数据，Sink是关键计算，注入漏洞。

污点分析具体规则

定义：关注的是，一个污点数据是否能流向sink点。或者说，指向sink点处的指针会不会指向污点数据。

污点分析更关心数据，而不是变量，是对数据打标签。

TA/PTA对比：污点分析与指针分析，一个是污点数据的流向，一个是抽象对象的流向。

指针分析其实就是盯着程序中的抽象对象的流向，

思想：

可把污点数据看作是

特殊的对象

source看作这些对象的allocation-site

借助指针分析来实现污点分析

标记：t_i表示调用点i(call site i)返回的污点数据，t_i指针集就包含普通对象+污点数据。

规则：

1. Source：先看CG图，如果程序有语句在l处调用了m方法，有调用边。条件是如果m属于分析的Source方法集合内，那么我们就把返回值标记为污点值tl，更新返回值r的指向。
2. Sink：在Sink的调用点检查就可以了。主要就是看调用点的调用目标方法，如果目标方法属于Sink集合，那么就开始检查参数，遍历参数，看参数他们的指针集。如果指针集之中发现了污点数据，那么就产生了TaintFlows，会报告说污点数据tj会流到m方法中。

示例：第3行产生新对象o11的同时，产生的污点数据t3；最终指针分析发现，t3会流向sink函数log()。

理解：

首先x指向o2，pw指向o11这个对象。由于getPassword方法是一个Source方法，那么就会触发处理source规则，会生成taint对象，上下文目前是在第三行，那么就是t3，加入到pw的指针集里面。

实现分析器用到：分析Java用Soot/WALA；分析C++用LLVM；有的用Datalog实现分析器（如DOOP分析框架）。

LLVM指针分析工具：SVF

14

Datalog语法，如何利用Datalog实现指针分析和污点分析。

本节课内容讲到了很多数据逻辑方面的应用，单上数理逻辑会觉得理论性太强，单上这节课的应用知识又觉得理论上不够严谨，总之算是一种互补。

Motivation

内容：了解命令式 vs 声明式语言，对比两种语言实现指针分析算法的优劣。

// 问题：从一群人中挑出成年人。
// 命令式语言(Imperative)：详细的命令机器怎么（How）去处理一件事情以达到你想要的结果（What）。如Java
Set<Person> selectAdults(Set<Person> persons) { 
  Set<Person> result = new HashSet<>();
  for (Person person : persons)
    if (person.getAge() >= 18)
      result.add(person);
    return result; 
}
// 声明式语言(Declarative)：只告诉你想要的结果（What），机器自己摸索过程（How）。如SQL，代码更简洁
SELECT * FROM Persons WHERE Age >= 18;

命令式语言—PTA：若采用命令式实现指针分析算法，实现复杂。需考虑worklist数据结构，是数组list还是链表，是先进先出还是先进后出；如何表示指针集合，hash集还是bit向量；如何关联PFG节点和指针；如何处理相关语句中的变量。

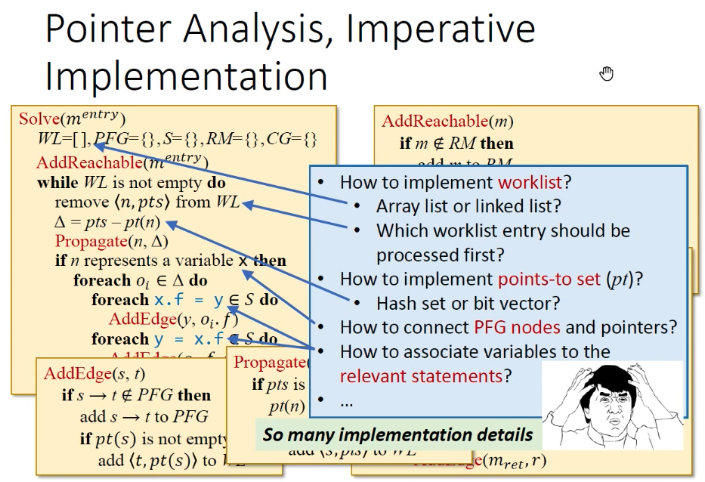
声明式语言—PTA：如何用声明式语言实现PTA？优点是简洁、可读性强、易于实现，例如Datalog。缺点是不方便表达复杂逻辑（Eg，for all全部满足）、不能控制性能。

Datalog介绍

Datalog（Data + Logic）：是声明式逻辑编程语言，可读性强，最初用于数据库。现在可用于程序分析、大数据、云计算。特点—没有副作用、没有控制流、没有函数、非图灵完备（精简了许多功能）。

Data

谓词，原子。

谓词Predicate：看作一系列陈述的集合，陈述某事情是不是事实（真假）。如Age表，表示一些人的年龄。

事实fact：特定值的组合。Eg，(“Xiaoming”, 18)。

原子Atom：P(X1, X2, ... , Xn)。P表示谓词名，Xi表示参数（又叫term，可以是变量或常量）。

Age("Xiaoming", 18) == true ；

Age("Alan", 23) == false。

Logic(Rule)

Rule：表示逻辑推导规则，若Body都为true，则Head为true。H <- B1, B2, ... ,Bn。H是Head，Bi是Body。 Eg，Adult(person) <- Age(person, age), age >= 18。

Rule要求：规则中的值要有限，如A(x) <- B(y), x > y；规则不能有悖论，如A(x) <- B(x), !A(x)。

Datalog中逻辑或：A或B都可推导出C，可写成C<-A. C<-B.或者C<-A;B.，与的优先级高于或。

Datalog中逻辑非：!B(...)。

Datalog谓词分类

EDB（extensional database）外延数据库：谓词需预先定义，关系不可变，可被当做输入。

IDB（intensional database）内涵数据库：谓词是根据规则建立的，关系是根据规则推导的，可被看作是是输出。

说明：H <- B1, B2, ... ,Bn，H只能是IDB，Bi可以是EDB或IDB。

递归性：Datalog支持递归，也即能够推导出自身。

Eg，

Reach(from, to) <- Edge(from, to)；

Reach(from, to) <- Reach(from, node), Edge(node, to).

Datalog程序运行

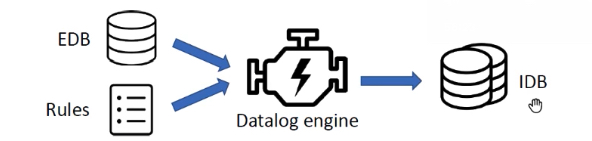
Datalog程序运行：输入EDB+rules到Datalog引擎，输出IDB。常用Datalog引擎——LogicBlox, Soufflé, XSB, Datomic, Flora-2。

Datalog程序性质：单调性、终止性。

Datalog实现指针分析

概念

EDB：程序句法上可获得的指针相关信息。如New / Assign / Store / Load语句。V-变量，F-域，O-对象。

上下文不敏感PTA示例

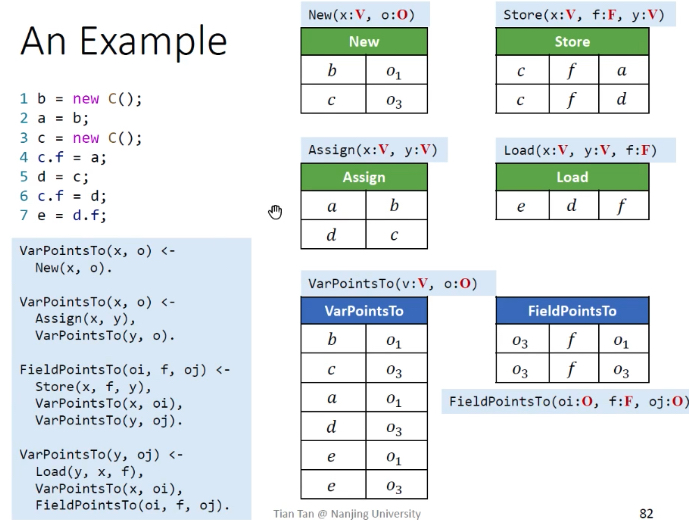
步骤：其实指令处理顺序不固定。

1. 首先将EDB（指令）表示成表格数据形式。
2. 处理New指令
3. 处理Assign指令
4. 处理Store指令
5. 处理Load指令

全程序指针分析-上下文敏感

call指令规则：S—指令，M—方法。共3条rule。

VCall：就是表示callsite，调用指令上下文位置l，变量x，方法k；

Dispatch：根据对象o，给定调用的方法k，去找到实际调用的方法m；

ThisVar：获取实际调用的方法m中的this变量

Reachable：表示方法m可达

CallGraph：表示l到m有一条边，可达

1. 首先找到调用的目标函数m，传递this指针。

2. 传递参数

形参->实参->o

3. 传返回值

三条规则的合影：

全程序指针分析：引入程序入口函数m。

Datalog实现污点分析

EDB谓词-输入：

• Source(m : M) —— 产生污点源的函数
• Sink(m : M) —— sink函数
• Taint(l : S, t : T) —— 关联某callsite l和它产生的污点数据t

IDB谓词-输出：

• TaintFlow(t : T, m : M) —— 表示污点数据t会流向sink函数m

规则：处理source和sink函数。

1. 有的调用图有多个main入口方法，咋办？

   将多个入口函数都加入到EntryMethod(m)即可。

2. 有没有datalog和传统结合的做法

   如chord（java+Datalog实现）

15

目标：以图可达性分析来进行程序分析，没有了数据流传播的过程。

Infeasible and Realizable Paths——基本概念

Infeasible Paths：CFG中存在，但是实际动态运行中不会执行到的路径，如不匹配的调用返回边。这种路径可能会影响到程序分析的结果，但静态分析不能完全判定路径是否可达，会造成误报。

也就是说，如果CG上存在假边，那么静态分析时，dataflow会绕着假边来流动，造成误报。我们希望假边尽可能少，误报也就尽可能少。

Realizable Paths：跨函数调用产生的return边和对应的call-site的call边匹配，这样的path。它可能不会被执行。

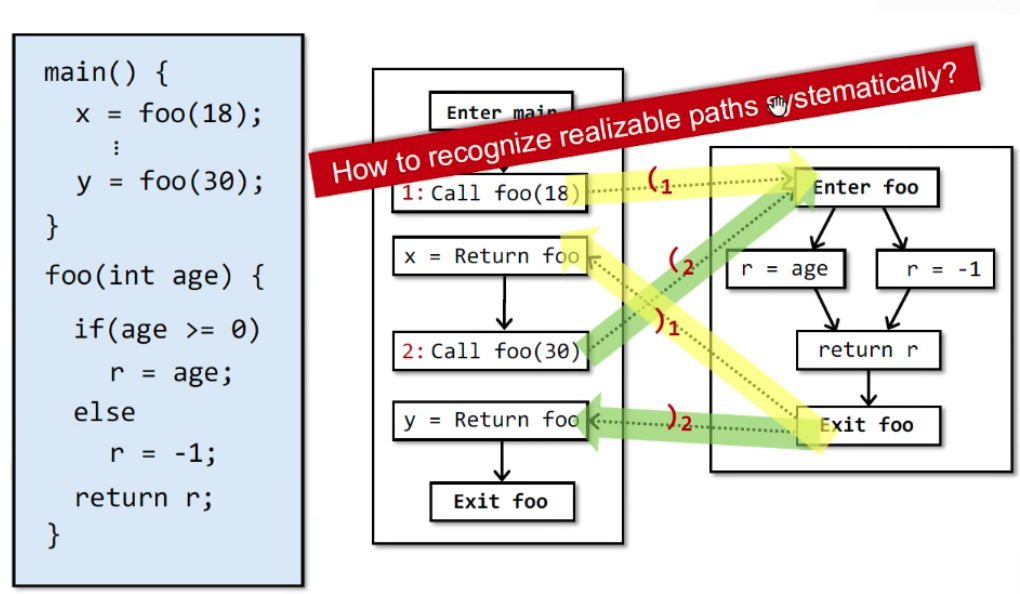
目标：识别Realizable path，避免沿着Unrealizable path来传播数据分析。沿着对儿来匹配，从1来回到1，从2来回到2。

方法：CFL-Reachablity。

CFL-Reachablity（IFDS的理论基础，识别Realizable path）

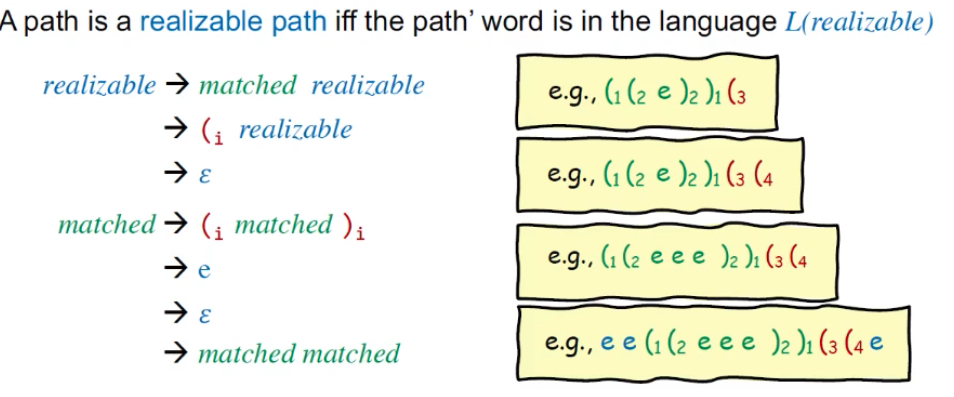
CFL-Reachablity：path连接A和B，或者说A能到达B，当且仅当path所有边的labels连接起来 是context-free language（CFL）中的一个word（或者说经过CFG语法变换之后可以得到该path word）。CFL是编译原理中的概念，遵循CFG语法。

简单来说：在边上添加label，那么一个路径realizable即这个路径上的边label组成了一个word，这个word是符合定义的上下文无关文法（CFG）的。

理解：

S可以无条件滴替换为asb，也可以无条件地替换ɛ。

部分括号匹配问题（Partially Balanced-Parenthesis）：利用CFL来解决括号匹配问题，以识别Realizable path。

• 部分——有)i一定要有(i，反之有(i不一定要有)i，也即可以调用子函数而不返回。
• 对于每个调用点i，将其调用边加 (i 的标签，将其返回边加 )i的标签；
• 标记，调用边——(i；返回边——)i；其他边——e。

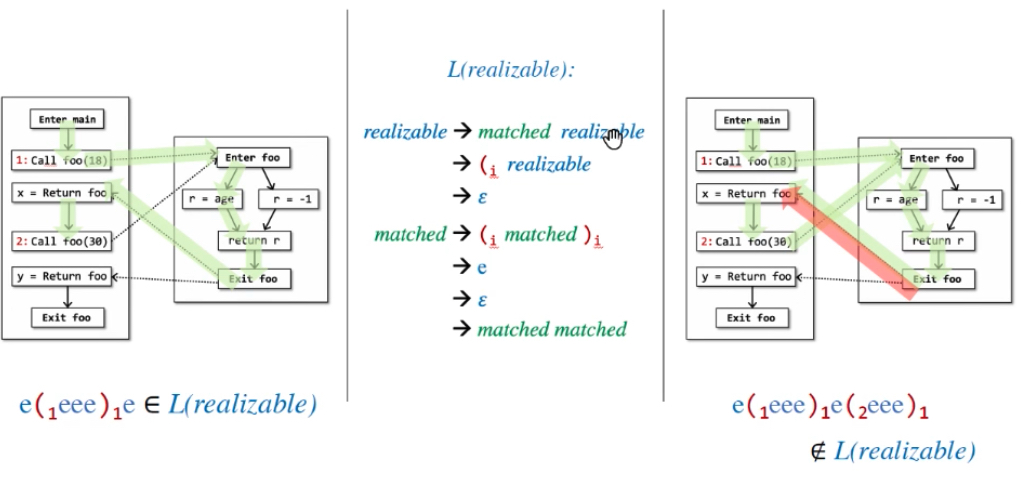
CFL-Reachablity：若path word（所有edge的label连起来组成的单词）可用CFL L(realizable)表示（可进行各种替换），则为Realizable Path。

示例如下，(1(2e)2)1(3就是边的label相连接形成的，绿色是可匹配的部分，realizable可被替换为matched realizable、(i realizable、ɛ。语法替换规则如下，这也是一个CFL语言示例：

示例：

看边就行了

IFDS

IFDS含义：

Interprocedural，Finite，Distributive，Subset - Problem

Interprocedural—全程序分析

Finite—域有限（如live variables、definitions）

Distributive—Transfer Function满足f(aub)=f(a)uf(b)，gen&kill一类的都满足

Subset—子集问题，面向主流程序问题

图可达性

利用图可达性的程序分析框架：采用的操作——Meet-Over-All-Realizable-Paths（MRP），MRP比MOP更加精确，范围更小。

MOP对所有路径进行meet操作，MRP只对realizable path进行meet操作，更准确。

Supergraph（之前叫iCFG）& Flow Functions

IFDS步骤一：构造Supergraph

说明：之前叫iCFG，给每个node定义transfer function；现在叫做supergraph，给每个edge定义transfer function。

Supergraph：G=(N, E*)。

• G*包含所有的流图G1, G2, … （每个函数对应一个流图，本例对应Gmain和Gp）；
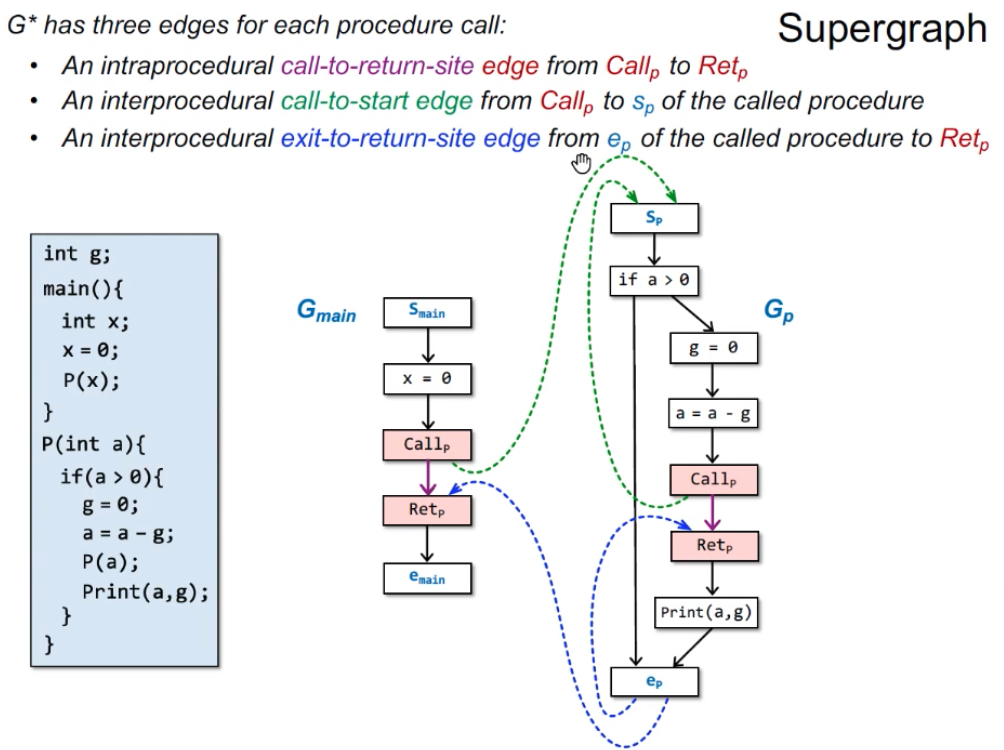
• 每个流图Gp都有个开始节点sp和退出节点ep；
• 每个函数调用包含调用节点Callp 和 返回节点Retp。
• 函数调用有3类边：
  • 过程内call-to-return-site边，从Callp→Retp；
  • 过程间call-to-start边，从Callp→sp（sp是被调用函数的开头）；
  • 过程间exit-to-return-site边，从ep→Retp（ep是被调用函数的结尾）。

IFDS步骤一：设计流函数 flow functions

示例：

• call-to-callee把与callee直接相关信息传递进去，如用形参替换实参；
• exit-to-return边把形参相关信息剔除；
• call-to-return-site只传递局部变量，排除全局变量g，降低误报。全局变量已经传入到被调用函数进行处理了，全局变量是否被初始化取决于被调用函数。

例子:

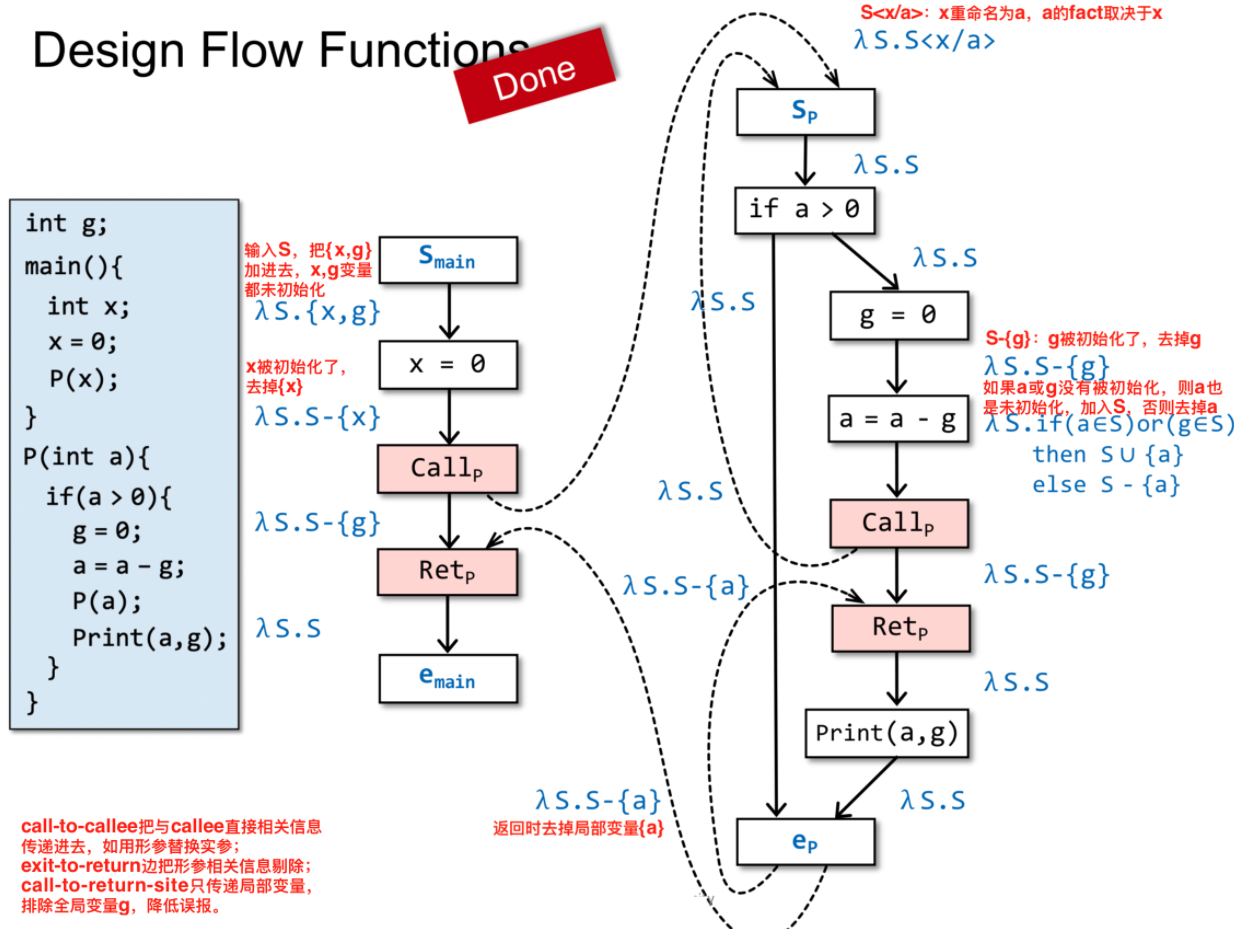
Exploded Supergraph and Tabulation Algorithm

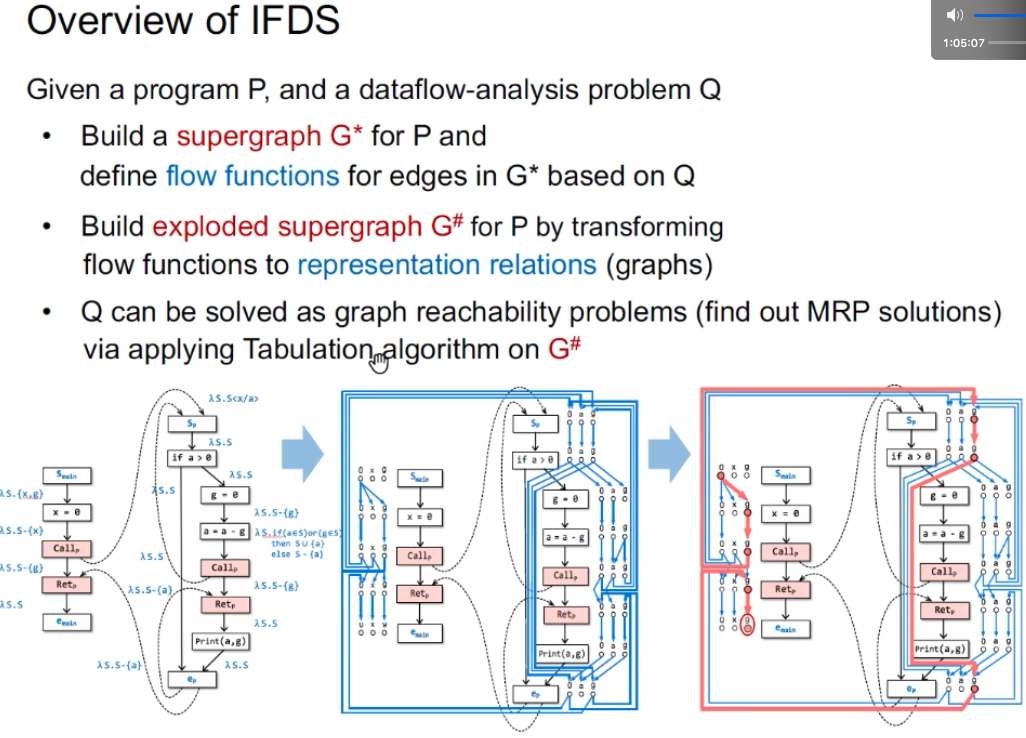
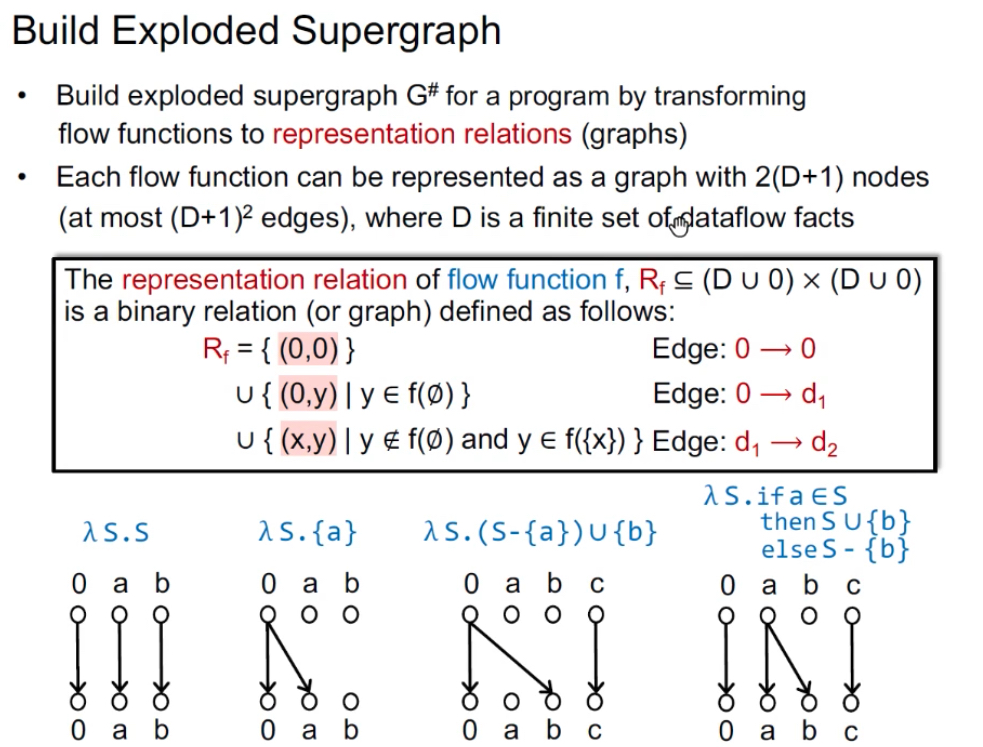
IFDS步骤二：构造exploded supergraph G#

Exploded SupergraphG#：将trans func转换成边的关系representation relations（graph），每个流函数变成了有2(D+1)个节点，边数最多(D+1)2，D表示dataflow facts元素个数（如待分析的变量个数）。G*中每个结点n被分解成D+1个结点，每条边n1→n2被分解成representation relation。

示例：

• （1）输入S是什么输出就是什么，1/3；
• （2）无论什么输入，都输出{a}，1/2；
• （3）b是无条件产生，所以0→b，a不能往下传了，b已经从0可达了就不用加b→b，c不受影响，也即无论有关a和b的事实之前是什么样，都不再重要；
• （4）b通过a得到所以a→b，不影响a、c的传递。注意，这里的值不是说变量在程序中真正的值是多少，而是说有关此变量的数据流事实的值是什么，如a的值可以为被初始化了和未被初始化两种，对应的集合即不包括和包括a。

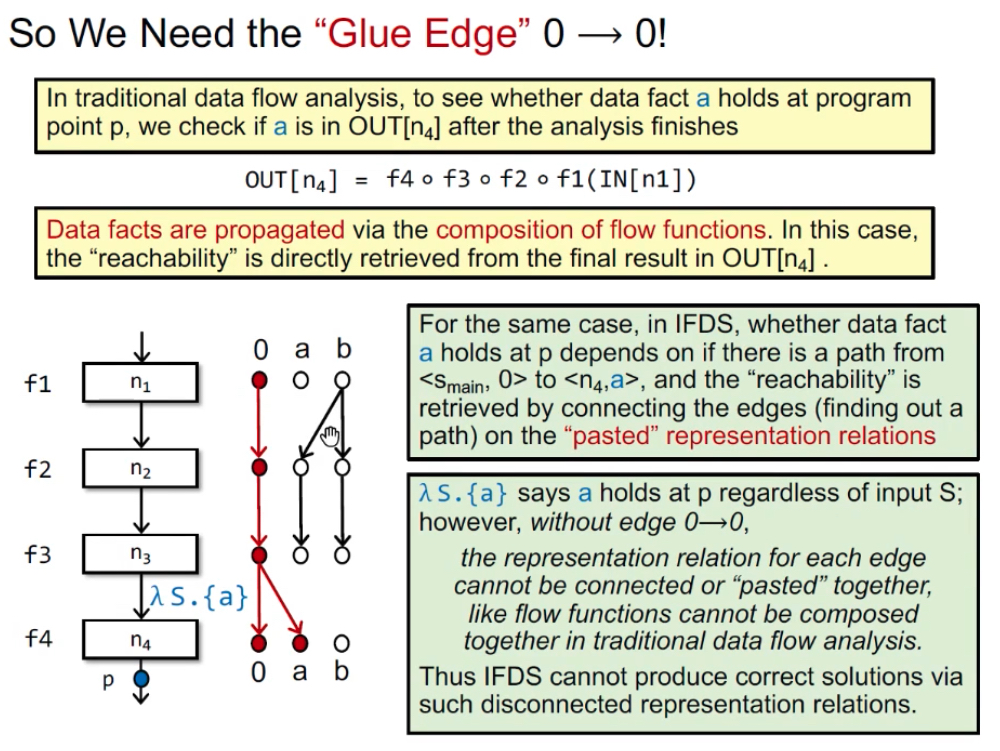
问题：为什么需要0→0的边？以往数据流分析中，确定程序点（结点）p是否包含data fact a，是看a是否在OUT[p]中；IFDS中，是看<s_main, 0>是否能到达<p, a>。如果没有0→0的边，则无法完全连通，所以0→0又称为Glue Edge。

构建G#示例：最后能从<s_main, 0>→<e_main, g>（要通过realizable paths），则e_main点的g是可能未初始化的。emain处的x和n_Print(a,g)处的g都是初始化过的，因为从s_main不可达（不能通过non-realizable paths——绿色线）。

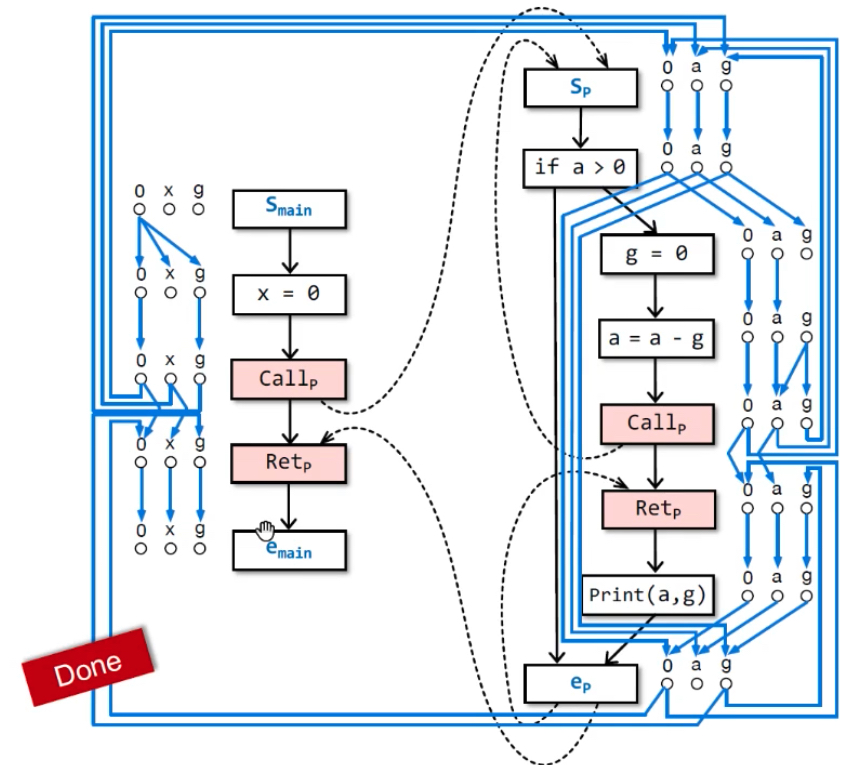
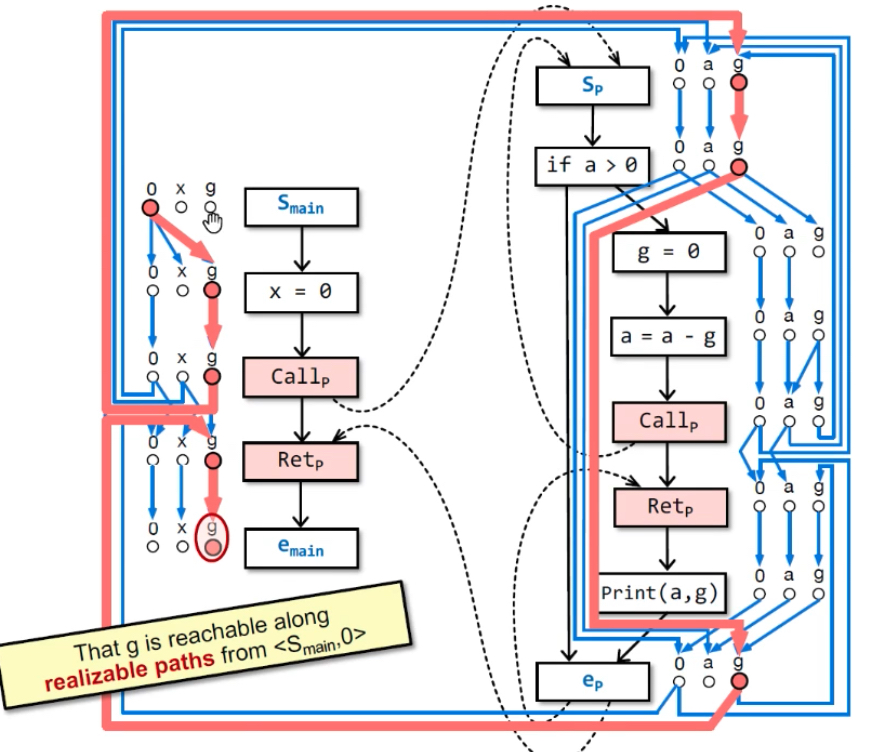
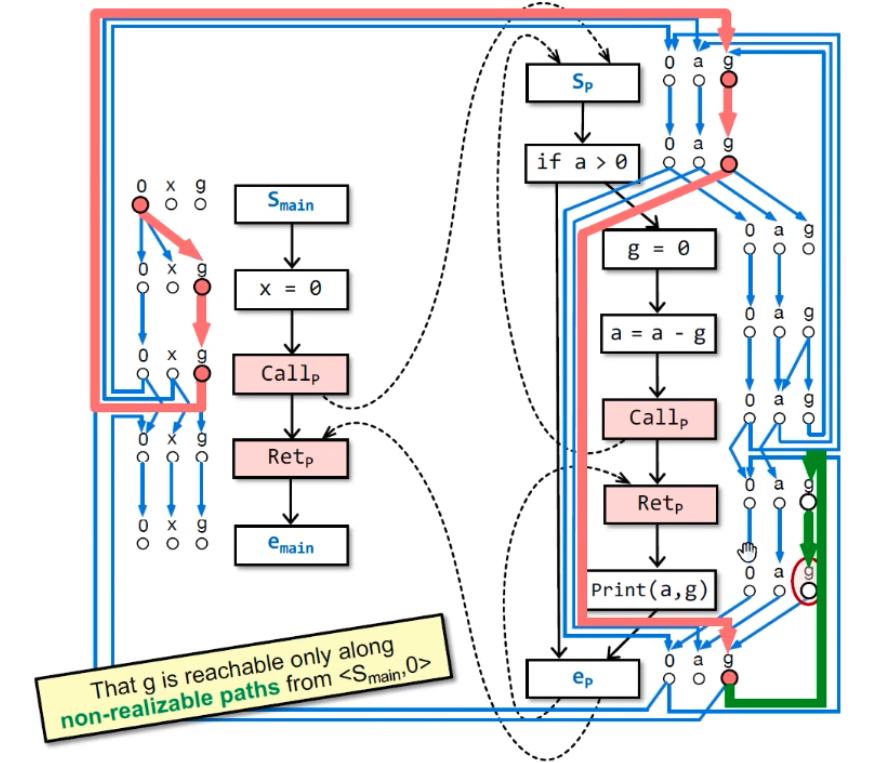
不可达原因：括号没匹配上，return-site没有匹配

IFDS步骤三：Tabulation算法——判断是否可达

Tabulation算法工作原理：假设只关注1个data fact，p’ 被 p 和 p’’ 同时调用。

• p’的入口点一定是自己连自己，一定可达

• 处理括号匹配：每次处理到返回点ep’时，开始括号匹配（call-to-return匹配），找到调用点(Callp， Callp’’)和相应的返回点(Retp，Retp’’)。

• 处理总结边——SummaryEdge：总结边—<Call,dm>→<Ret,dn>，表示dm通过调用p’能到达pn，用来避免重复处理p和p’’中调用同一函数p’（优化）。

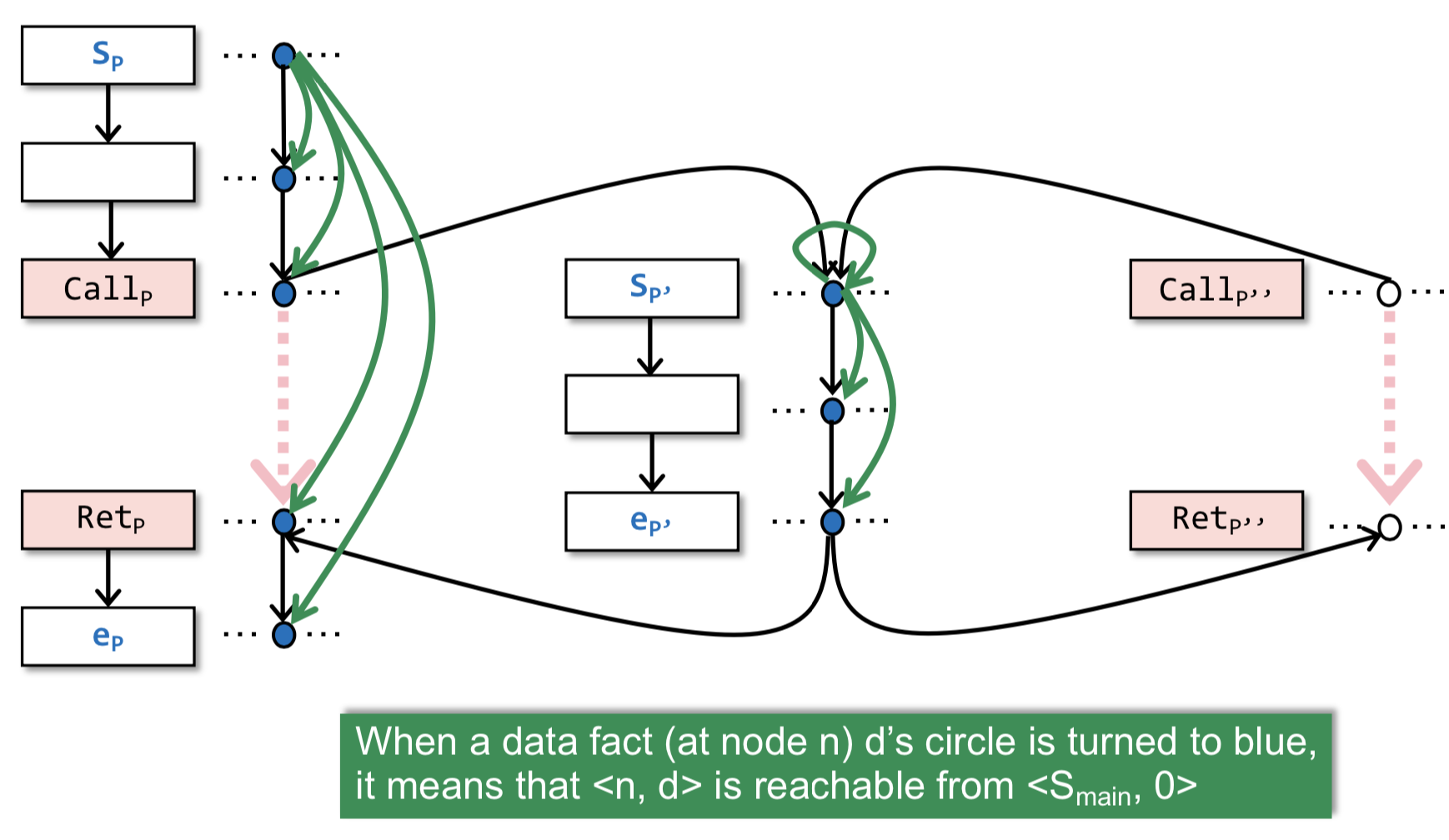
Tabulation算法优点：传统的worklist算法是利用了queue的特性，每次循环只考虑与被改变值结点的相关结点。论文中用于解决图可达问题的Tabulation 算法是基于worklist的动态规划算法，比传统worklist算法考虑interprocedure问题更精确也更省时。

Understanding the Distributivity of IFDS

结论：不能用IFDS进行常量传播分析、指针分析。

原因：由IFDS的框架决定，一次只能处理1个变量。例如，表示若x和y都存在则会冲突，无法表示这种关系。不满足F(x^y)=F(x)^F(y)。

总结：给定语句S，如果输出取决于多个输入的data fact，则该分析不具备可分配性，不能用IFDS表达。IFDS中，每个data fact（圆圈）与其传播（边）都可以各自处理，且不影响最终结果。

IDE：IDE（Interprocedural，Distributive，Environment problem）作为IFDS的优化，可以解决infinite的问题，但是仍需满足distributive。

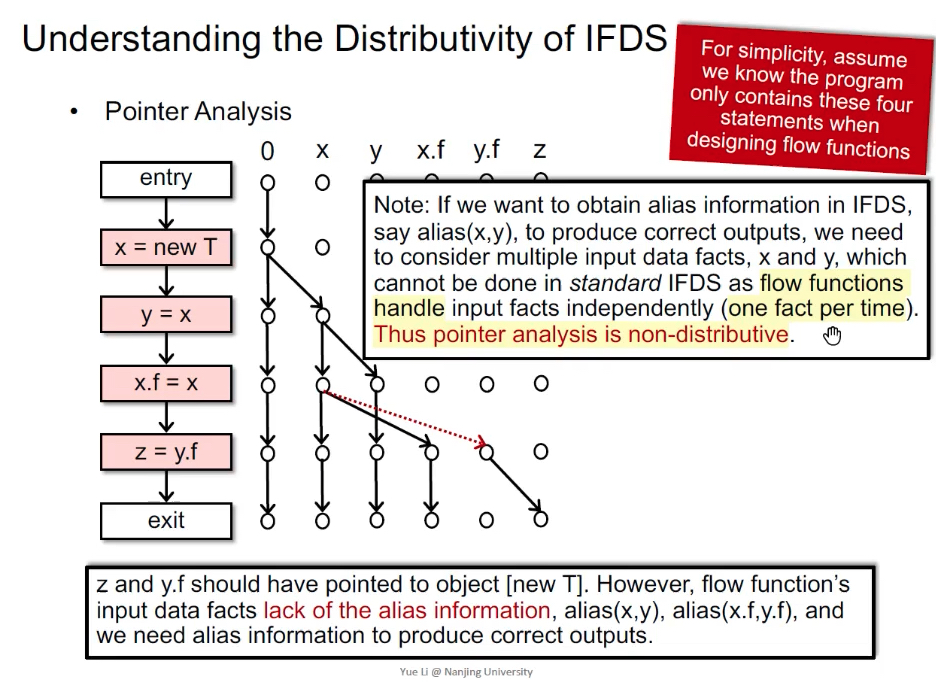
指针分析：箭头表示变量是否指向new T，但由于缺乏别名信息alias(x,y) / alias(x.f,y.f)，导致分析结果错误。也就是说正常应该有一个红色的虚线边，但是由于缺少了别名分析，导致分析错误。

传统IFDS是每次只感知一个input，对于这个例子来说需要同时知道x和y是否指向同一个内存对象，这其实是两个input。就不满足可分配的必要特性，所以可以说指针分析是non-distributive的。

归根结底，要想在IFDS中获取别名信息alias(x,y)，需要考虑多个输入data fact（x、y），所以不能用IFDS。

16

Soundness & Soundiness

分析真实复杂程序时，产生的问题都与Soundiness有关，是最前沿的topic之一。

Soundness：保守估计，分析结果能包含程序所有可能的执行，OVER。学术界和工业界都做不到。

复杂语言特性：导致分析结果不精确。

• Java：Reflection, native code, dynamic class loading, etc.
• JavaScript：eval（执行任意命令）, document object model (DOM，和DOM加护), etc.
• C/C++：Pointer arithmetic（指针地址加或乘操作）, function pointers, etc.

现状：有些文章不提这类问题，或者随意一提（如eval）。极具误导性，导致相信该工具很sound，且影响专家的评判。

Soundiness：直观相信的”truth”，但没有任何事实和证据。

sound analysis：分析大部分都是sound的，并且对于hard-to-analysis部分来说，明确说出来是怎么处理的。

词语对比：

• sound analysis：能捕捉所有动态运行行为，纯理想化分析。
• soundy analysis：目标是捕捉所有动态行为，但对于某些复杂语言特性可以unsound。
• unsound analysis：为了效率、精度，故意不处理某些行为。

复杂语言特性一：Java Reflection—反射

什么是Java反射

Java Reflection：反射机制很重要的一点就是“运行时”，其使得我们可以在程序运行时加载、探索以及使用编译期间完全未知的 .class 文件。换句话说，Java 程序可以加载一个运行时才得知名称的 .class 文件，然后获悉其完整构造，并生成其对象实体、或对其 fields（变量）设值、或调用其 methods（方法）。

三个MetaObject：

Class-class，Method-method，Field-field分别对应。

反射世界虽然复杂，但是离不开第一步入口：获取Class对象。

说明：非反射代码在编译时就能确定对象；反射代码在运行时才确定对象，如c指向什么，”Person”也可能是的字符串指针，很难静态分析。分析该类代码很有必要，如弄清对象到底调用了哪个目标函数、对象域的指向关系等。

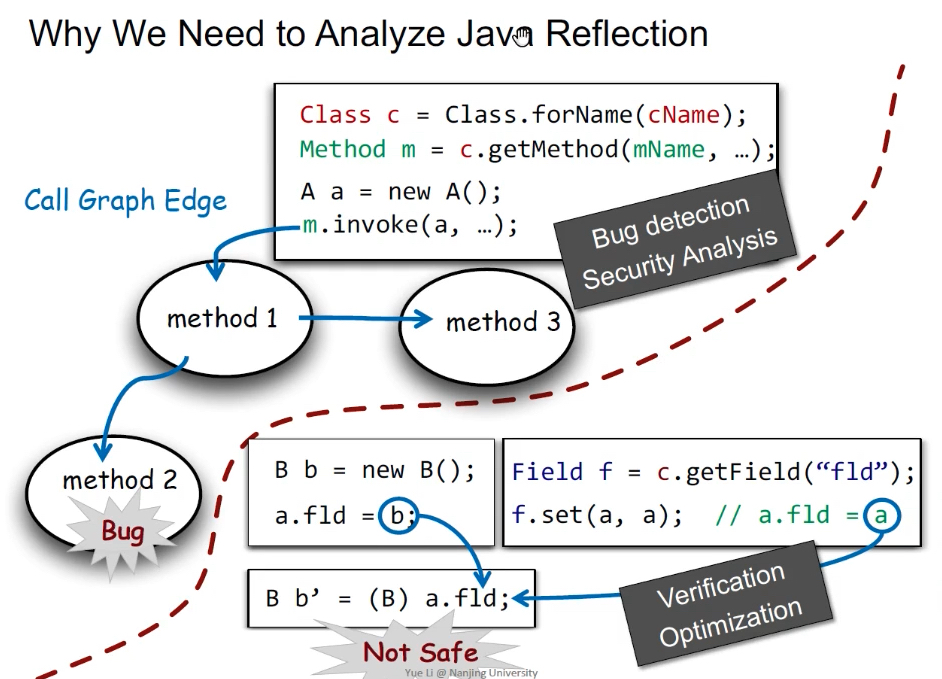
分析方法

分析方法：String Contant analysis + Pointer Analysis（Reflection Analysis for Java——APLAS 2005）。

示例：目标是分析m调用的目标函数。

• 找到m的定义点，即Method m = c.getMethod(mName, ...);
• 通过String Contant analysis找到mName指向内容
• 通过指针分析找到c指向内容
• 通过String Contant analysis找到cName指向内容
• 知道了是调用Person类的setName函数

问题：若字符串的值无法通过静态分析得到，则反射目标不能求解。Eg，字符串来自配置文件、网络、命令行、复杂字符串处理、动态生成、加密。

改进

解决方法：Type Inference + String analysis + Pointer Analysis（Self-Inferencing Reflection Resolution for Java——ECOOP 2014，李樾，谭添老师的成果）。

在创造点不可推，但在使用点可推。

示例：【搜集隐藏线索】类名依赖cmd参数，解不出来；但在调用点，通过Java的类型系统推导parameters，发现parameters是this指针。

推出结论就是，175行的目标函数肯定有1个参数，且这个参数的声明类型要么是FrameworkCommandInterpreter要么是其子类。

结果推断出50个反射目标函数，48个为true。

最新工作：Understanding and Analyzing Java Reflection (TOSEM 2019) Yue Li, Tian Tan, Jingling Xue。不仅求解反射对象更准确更多，而且能说出哪里解的不准。

常用方法：Taming reflection: Aiding static analysis in the presence of reflection and custom class loaders (ICSE 2011)。利用动态分析来解，缺点是测试用例的覆盖路径有限，优点是只要解出来，结果都为真。

复杂语言特性二：Native Code

Native Code：一个Native Method就是一个java调用非java代码的接口。该方法的实现由非java语言实现，已被编译为特定于处理器的机器码的代码，这些代码可以直接被虚拟机执行，与字节码的区别：虚拟机是一个把通用字节码转换成用于特定处理器的本地代码的程序，比如C。这个特征并非java所特有，很多其它的编程语言都有这一机制，比如在C++中，你可以用extern “C”告知C++编译器去调用一个C的函数。

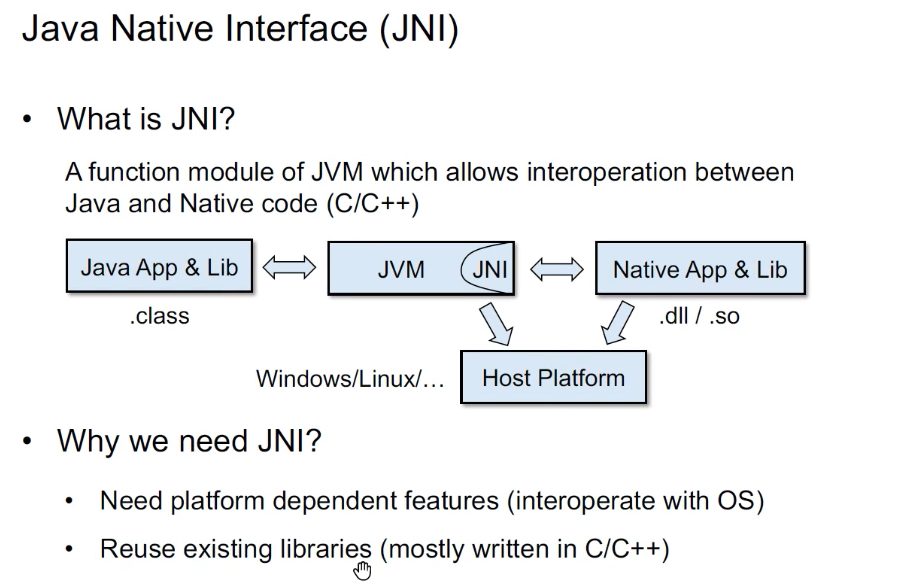
Java Native Interface(JNI)：是一种编程框架（函数模型，反映参数格式等），使得Java虚拟机中的Java程序可以调用本地应用/或库，也可以被其他程序调用。 本地程序一般是用其它语言（C、C++或汇编语言等）编写的，并且被编译为基于本机硬件和操作系统的程序。

也就是说，Java应用或者Lib包都是class文件，可以通过JVM内部的JNI接口与Native App&Lib原生来交互。

示例：先加载Native库，声明Native函数，*env变量可以在Native代码中用于创建对象、访问域、调用Java中的方法等，支持230个JNI函数。问题是跨语言之后，如何静态分析je.guessMe()这个调用？

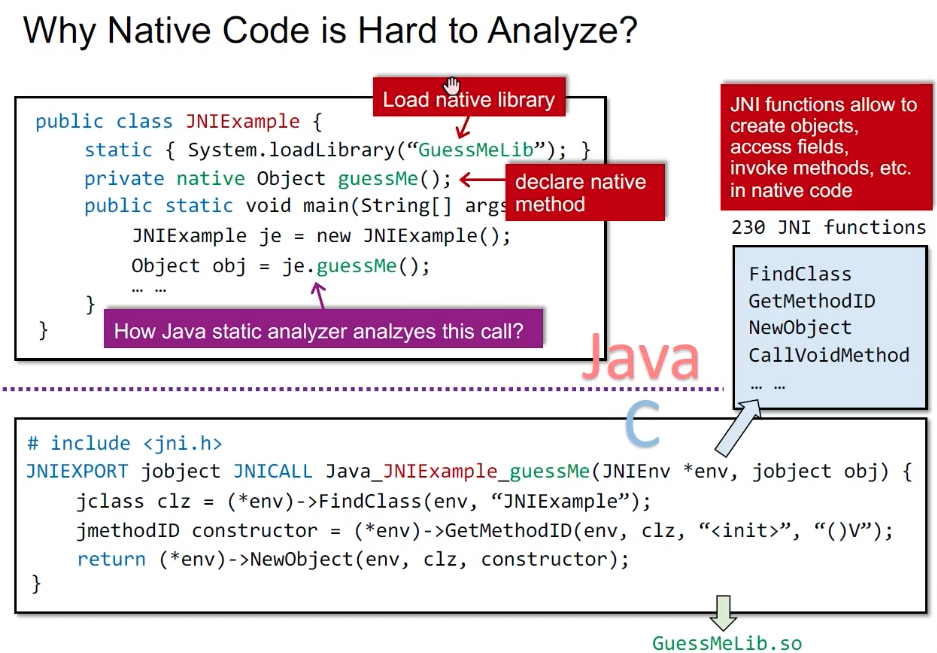
方法：对重要的native code手动建模。例如，对经常调用的arraycopy()函数进行建模，建模后就是一个拷贝循环，但从指针分析角度来讲，看到这个循环，我们就把数组指针进行传递。

参考

bsauce